Kezdőlap


Feladat:	1404. fizika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Kalcsú Zoltán
Füzet:	1977/szeptember, 38 - 39. oldal		PDF \| MathML
Témakör(ök):	Kondenzátorok kapcsolása, Feladat
Hivatkozás(ok):	Feladatok: 1976/december: 1404. fizika feladat

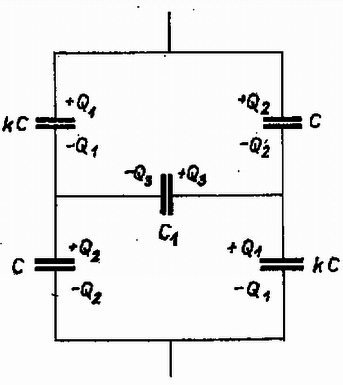
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az egyes kondenzátorlemezeken levő töltést az ábrán tüntették fel, az elrendezés szimmetriáit is felhasználva.

A kapcsolás két vége között:

\begin{matrix} U = Q_{1} / (k C) + Q_{2} / C \end{matrix}

(1)

feszültségkülönbség van, és a rendszer

Q = Q_{1} + Q_{2}

külső töltést tárol. A

C_{1}

kapacitás tölltése a töltésmegmaradás miatt

Q_{3} = Q_{2} = Q_{1}

. A

C_{1}

kondenzátoron levő töltés és feszültségkülönbség közötti összefüggés értelmében

\begin{matrix} Q_{1} / (k C) - Q_{2} / C = (Q_{2} - Q_{1}) / C_{1}, \end{matrix}

(2)

amiből

\begin{matrix} Q_{2} = Q_{1} \frac{k C + C_{1}}{k C + k C_{1}} . \end{matrix}

(3)

A kapcsolás eredő kapacitása

\begin{matrix} C_{x} = \frac{Q}{U} = \frac{Q_{1} + Q_{2}}{U}, \end{matrix}

(4)

ami az (1) és (3) összefüggések felhasználásával

\begin{matrix} C_{x} = C \frac{2 k C + (k + 1) C_{1}}{2 C_{1} + (1 + k) C} \end{matrix}

(5)

alakban irható. Ha az eredő kapacitás

C_{x} = C, akkor C_{1} = - C

, ami lehetetlen;
b)

C_{x} = k C, akkor C_{1} = - k C

, ami szintén lehetetlen;
c)

C_{x} = C_{1}, akkor C_{1} = \sqrt[]{k} C

Kalcsú Zoltán (Szolnok, Verseghy F. Gimn., IV. o. t.)