Kezdőlap


Feladat:	1393. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Farkas Ferenc , Halász Ilona , Héder János , Németh Gábor
Füzet:	1977/április, 184 - 185. oldal		PDF \| MathML
Témakör(ök):	Kúpinga, Körmozgás (Tömegpont mozgásegyenlete), Rugalmas erő, Nehézségi erő, Centrifugális erő, Feladat
Hivatkozás(ok):	Feladatok: 1976/november: 1393. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mivel a test körpályán mozog az $m g$ súlyerő és az $R$ rugóerő hatására, mozgásegyenletei a következők (l. az ábrát):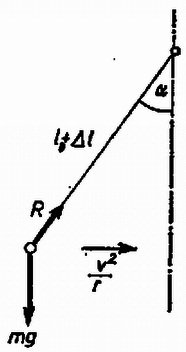

\begin{matrix} m v^{2} / r = & R sin α, \\ 0 = & R cos α - m g . \end{matrix}

A körpálya sugara

\begin{matrix} r = (l_{0} + Δ l) \cdot sin α, \end{matrix}

ahol

Δ l

a rugó megnyúlása az

R

erő hatására,

Δ l = R / D

.
Ezekből az összefüggésekből a tömeg sebessége tetszőleges

α

szög esetén kifejezhető:

\begin{matrix} v^{2} = (\frac{m g}{D cos α} + l_{0}) \cdot g tg α sin α . \end{matrix}

α

helyére

α_{1} = 30^{\circ}

-ot, ill.

α_{2} = 60^{\circ}

-ot helyettesítve megkaphatjuk a kétféle szöghelyzet eléréséhez szükséges sebességek arányát:

\begin{matrix} k = \frac{v_{2}}{v_{1}} = 3 \sqrt[]{\frac{2 m g + D l_{0}}{2 m g + \sqrt[]{3} \cdot D l_{0}}} . \end{matrix}

Halász Ilona (Dunaharaszti, Baktay E. Gimn., III. o. t.)

Megjegyzés. Vizsgáljuk meg, hogy

α_{1} = 30^{\circ}

α_{2} = 60^{\circ}

esetén

k

milyen értékek között változhat! Mivel

\begin{matrix} \frac{1}{\sqrt[]{3}} = \frac{1}{\sqrt[]{3}} \frac{2 m g + \sqrt[]{3} D l_{0}}{2 m g + \sqrt[]{3} D l_{0}} ≦ \frac{1}{\sqrt[]{3}} \frac{\sqrt[]{3} \cdot 2 m g + \sqrt[]{3} D l_{0}}{2 m g + \sqrt[]{3} D l_{0}} = \frac{2 m g + D l_{0}}{2 m g + \sqrt[]{3} D l_{0}} ≦ \frac{2 m g + \sqrt[]{3} D l_{0}}{2 m g + \sqrt[]{3} D l_{0}} = 1, \end{matrix}

azért

\begin{matrix} 2, 28 \approx \sqrt[]{3 \sqrt[]{3}} ≦ k = 3 \sqrt[]{\frac{2 m g + D l_{0}}{2 m g + \sqrt[]{3} D l_{0}}} ≦ 3. \end{matrix}

D l_{0} ≫ m g

, vagyis a rugó alig nyúlik meg,

k = \sqrt[]{3 \sqrt[]{3}} \approx 2, 28

; ha

D l_{0} ≪ m g

, azaz a rugó nagyon ,,nyúlékony'', akkor

k = 3

. A sebességek aránya tehát

D l_{0}

és

m g

arányától függően egy elég szűk intervallumban,

2, 28

és 3 között változhat.

Farkas Ferenc (Szeged, Radnóti M. Gimn., II. o. t.)