Feladat: 1389. fizika feladat Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Tóth András 
Füzet: 1977/március, 138 - 139. oldal  PDF  |  MathML 
Témakör(ök): Kúpinga, Nehézségi erő, Térerősség és erő, Centrifugális erő, Körmozgás (Tömegpont mozgásegyenlete), Feladat
Hivatkozás(ok):Feladatok: 1976/október: 1389. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A G súlyú, Q töltésű részecskére a kötélerőn kívül az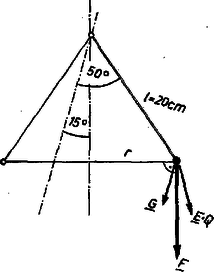

F=G+QE
erő hat. Az elektromos erőtér és a nehézségi erőtér homogén, ezért F a körpálya bármely pontján azonos.
 

 

A kúpinga mozgása ezért ugyanolyan, mintha egy F ,,súlyú'' részecske mozgását vizsgálnánk. Ebből következik, hogy a kúptengelye az F vektor irányával párhuzamos lesz. A konkrét adatokkal |G|=mg=9,8⋅10-2N;Q|E|=9,8⋅10-2N; tehát |G|=|E|Q. Mivel a közöttük levő szög 30∘,F a függőlegessel 15∘-os szöget zár be. A kúp félnyílásszöge így 50∘-15∘=35∘, s a vízszintessel bezárt legkisebb szög 35∘-15∘=20∘.
Az F erő nagysága
|F|=2⋅mgcos15∘.
A szokásos kúpingához hasonlóan a körmozgás feltétele:
mv2/r=|F|tg35∘,r=l⋅sin35∘.


Ebből
v2=|F|tg35∘⋅l⋅sin35∘m,v=2glcos15∘sin235∘cos35∘.
A számadatokkal
v=1,23m/s.
(E más típusú irányítása pl. ↗ vagy ↙ esetén nem teljesülne az a feltétel, hogy az 50∘-os szög a legnagyobb függőlegessel bezárt szög.)
 

  Tóth András (Pécs, Nagy L. Gimn., IV. o. t.)
 

Megjegyzés. A feladat szövegébe kitűzéskor sajtóhiba került. Az elektrosztatikus térerősség közölt 2⋅10-4V/m-es értéke az inga mozgására igen kis hatással van. Természetesen bármelyik adattal számolt is a megoldó, a helyes megoldásért a maximális pontszámot kapta.