Kezdőlap


Feladat:	1375. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Győri András
Füzet:	1977/február, 87 - 89. oldal		PDF \| MathML
Témakör(ök):	Hajítások, Egyenletes körmozgás, Feladat
Hivatkozás(ok):	Feladatok: 1976/szeptember: 1375. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A lövedék az ábrán $B$ -vel jelölt ponton hagyja el a henger belsejét.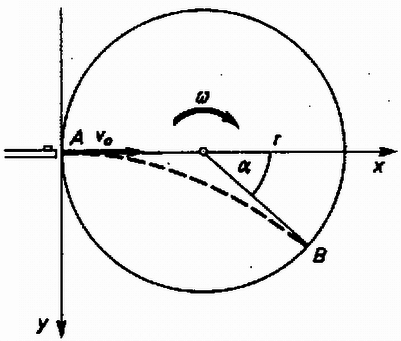

Pályája az

A

és

B

pontok között parabola, amelyet az ábra szerint felvett koordináta-rendszerben a következő paraméteres egyenletrendszerrel írhatunk fel:

\begin{matrix} y = (g / 2) t^{2}, \\ x = v_{0} t, \end{matrix}

ahol

x

és

y

a lövedék koordinátái a

t

időpontban,

v_{0}

pedig az

A

pontban a lövedék vízszintes irányú kezdősebessége. A papírhenger átlyukasztásához szükséges energiát elhanyagoljuk. A lövedék

t'

idő alatt jut el a

B

pontba, amelynek koordinátái az

α

szög segítségével egyszerűen felírhatók. Így

\begin{matrix} (g / 2) t'^{2} = r sin α, & (1) \\ v_{0} t' = r (1 + cos α) . & (2) \end{matrix}

Tegyük fel, hogy

α

elég kicsi, ekkor

sin α \approx α

és

cos α \approx 1

(ezek

1

%-os pontossággal teljesülnek, ha

α < 0, 1

.) Ezeknek a közelítéseknek a felhasználásával egyszerűen megoldható egyenletrendszert kapunk. A megoldások:

\begin{matrix} t' = 2 r / v_{0}; α = 2 g r / v_{0}^{2} . \end{matrix}

A lövedék akkor üt egy lyukat, ha a henger

t'

idő alatt úgy fordul el, hogy az

A

pont kerül

B

helyére. Az ábrán jelölt forgásirányt véve pozitívnak, a hengernek tehát

\begin{matrix} α \pm (2 n + 1) π (n = 0, 1, 2, ...) \end{matrix}

szöggel kell elfordulnia. Így a henger szögsebessége

\begin{matrix} ω = \frac{α \pm (2 n + 1) π}{t'} = \frac{g}{v_{0}} \pm (2 n + 1) \frac{π v_{0}}{2 r} . \end{matrix}

Mint említettük, ez a megoldás akkor ad jó közelítést, ha

α < 0, 1

azaz ha

v_{0} > \sqrt[]{20 g r}

Győri András (Győr, Révai M. Gimn., III. o. t.)

Megjegyzések. 1. Az (1) és (2) egyenletekből közelítés nélkül is számolhatunk tovább. (2) átrendezése után az egyenleteket négyzetre emeljük, majd összeadjuk:

\begin{matrix} \frac{g^{2} t'^{4}}{4} + v_{0}^{2} t'^{2} + r^{2} - 2 v_{0} t' r = r^{2} sin^{2} α + r^{2} cos^{2} α . \end{matrix}

A jobb és bal oldalról elhagyjuk

r^{2}

-et, és

t'

-vel osztjuk az egyenletet, hisz nyilván

t' \neq 0

\begin{matrix} (g^{2} / 4) t'^{3} + v_{0}^{2} t' - 2 v_{0} r = 0. \end{matrix}

Az így kapott hiányos harmadfokú egyenletnek csak egy valós gyöke van, ezt felírhatjuk a Cardano-formula segítségével:

\begin{matrix} t' = \sqrt[3]{\frac{4 v_{0}}{g^{2}}} (\sqrt[3]{r + \sqrt[]{r^{2} + \frac{4 v_{0}^{4}}{27 g^{2}}}} + \sqrt[3]{r - \sqrt[]{r^{2} + \frac{4 v_{0}^{4}}{27 g^{2}}}}) . \end{matrix}

Ennek ismeretében

α

-t is meghatározhatjuk, majd innen a már látott módon

ω

-t is megkapjuk:

\begin{matrix} ω = \frac{arc cos (v_{0} t' - r) \pm (2 n + 1) π}{t'}, (n = 0, 1, 2, ...) . \end{matrix}

Az így kapott kifejezés azonban nagyon bonyolult.
2. Az (1) és (2) egyenletekből paraméteres alakban egyszerűbb módon kaphatunk összefüggést

v_{0}

és

ω

között. (2)-ből beírjuk

t'

-t (1)-be, és átrendezés után

v_{0}

-ra kapjuk:

\begin{matrix} v_{0} = \sqrt[]{\frac{r g}{2 sin α}} (1 + cos α) . \end{matrix}

ω

felírásához még

t'

-t is meg kell határoznunk az egyenletrendszerből:

\begin{matrix} t' = \sqrt[]{\frac{2 r sin α}{g}} . \end{matrix}

Ennek ismeretében a szögsebesség:

\begin{matrix} ω = [α \pm (2 n + 1) π] \sqrt[]{\frac{g}{2 r sin α}}, (n = 0, 1, 2, ...) . \end{matrix}

Ezen képletek segítségével bármely

0 < α < π

-hoz meghatározhatjuk

ω

-t és

v_{0}

-t. Ha, pl.

α = 90^{\circ}

, akkor a lövedék kezdősebessége és a henger szögsebessége a következő:

\begin{matrix} v_{0} = \sqrt[]{\frac{r g}{2}}; ω = [\frac{π}{2} \pm (2 n + 1) π] \sqrt[]{\frac{g}{2 r}}, (n = 0, 1, 2, ...) . \end{matrix}