Kezdőlap


Feladat:	1362. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Binzberger Gábor , Faragó Béla , Harsányi Gábor , Tar József , Tóth Csaba , Zsigmond Géza
Füzet:	1976/december, 228 - 232. oldal		PDF \| MathML
Témakör(ök):	Felületi feszültségből származó erő, Görbületi nyomás, Közelítő számítások, numerikus módszerek, Függvények grafikus elemzése, Feladat
Hivatkozás(ok):	Feladatok: 1976/április: 1362. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Egy kis $Δ L$ hosszúságú fonaldarabra ‐ mivel ez két felülettel érintkezik ‐ a felületi feszültség miatt $2 α Δ L$ nagyságú erő hat.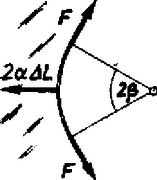

1. ábra

A görbült fonaldarabban ébredő erő egyensúlyozza ezt ki, így az 1. ábra szerint:

\begin{matrix} 2 F sin β = 2 α Δ L . \end{matrix}

Kis

β

esetén

sin β \approx β

, figyelembe véve továbbá azt, hogy

2 β R = Δ L

, kapjuk:

\begin{matrix} F = 2 α R . \end{matrix}

(1)

A fonalban végig ugyanakkora erő hat, így a fonál hártyával érintkező szakasza egy körív lesz.
Miután kiengedjük az edényből a folyadékot, a rudak és fonalak között egy hártya marad vissza. A fonalak alakja a kezdeti feltételektől függően különböző lehet, mint azt a továbbiakban részletesen végignézzük.
A felfüggesztett

l

hosszúságú rúdra a fonalak húzóereje, a folyadékhártya felületi feszültsége által keltett erő és a súlyerő hat. Attól függően, hogy a felületi feszültség okozta

2 α l

erő nagyobb-e a súlyerőnél, két esetet különböztethetünk meg. Ha

m g \leq 2 α l

, a fonál hozzásimul és részben hozzáfekszik a rudakhoz. Mindkét eseten belül további két eset lehetséges, attól függően, hogy a két

L

hosszúságú felfüggesztő fonál összeér-e.
i) Tárgyaljuk azt az esetet, amikor

m g \geq 2 α l

és a két felfüggesztő fonál nem ér össze. Ekkor a 2. ábrán látható elrendezés jön létre.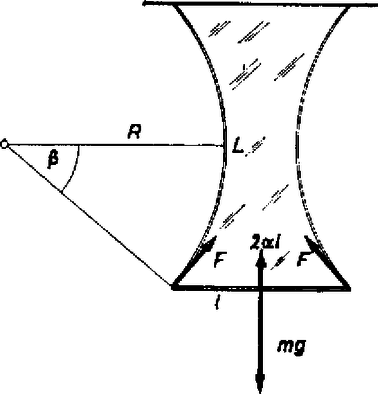

2. ábra

Az ábra jelölésével felírva a rúdra ható erők egyensúlyát:

\begin{matrix} m g = 2 α l + 2 F cos β . \end{matrix}

(2)

Tudjuk továbbá a bevezetőből a fonalban ható erő és a görbület kapcsolatát:

\begin{matrix} F = 2 α R . \end{matrix}

(3)

Ismerjük a felfüggesztő fonalak hosszát is:

\begin{matrix} L = 2 R β . \end{matrix}

(4)

(3) és (4) felhasználásával így alakul a (2) egyenlet:

\begin{matrix} \frac{cos β}{β} = \frac{m g - 2 α l}{2 α L} . \end{matrix}

(5)

m g ≫ 2 α (l + L)

, akkor

β

kis szög lesz, ekkor használhatjuk a

cos β \approx 1 - (β^{2} / 2)

helyettesítést, az így kapott másodfokú egyenlet gyöke:

\begin{matrix} β = \sqrt[]{{(\frac{m g - 2 α l}{2 α L})}^{2} + 2} - \frac{m g - 2 α l}{2 α L} . \end{matrix}

Egyéb esetekben pl. grafikus úton tudjuk megoldani az egyenletet.

β

ismeretében a (4) egyenlet felhasználásával meghatározhatjuk a görbületi sugarat is. A rúd emelkedése az ábra jelöléseivel:

\begin{matrix} Δ h = L - 2 R sin β, \end{matrix}

felhasználva a (4) egyenletet:

\begin{matrix} Δ h = L (1 - \frac{sin β}{β}) . \end{matrix}

Ezt az (5) egyenlet megoldása nélkül is meg tudjuk határozni, mivel

sin β = \sqrt[]{1 - cos^{2} β}

, így:

\begin{matrix} Δ h = L (1 - \sqrt[]{1 - {(\frac{m g - 2 α l}{2 α L})}^{2}}) . \end{matrix}

Ez a megoldás akkor helyes, ha a fonalak nem érnek össze, azaz ha

\begin{matrix} 2 (R - R cos β) < l, átírva (L / β) (1 - cos β) < l . \end{matrix}

(6)

ii) Legyen továbbra is

m g \geq 2 α l

, de a fonalak most érjenek össze. Ekkor a 3. ábrán látható helyzet jön létre.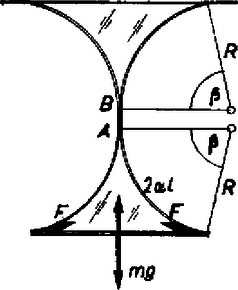

3. ábra

A (2) és (3) egyenletek most is érvényesek. (4) helyett azonban most más feltételt kell keresni. Az

A

és

B

pontok között a két fonal tartja csak a rudat, így az új egyenlet:

\begin{matrix} F = m g / 2. \end{matrix}

(7)

(2)-ből most (7) és (3) felhasználásával a következőt kapjuk:

\begin{matrix} cos β = \frac{m g - 2 α l}{m g} . \end{matrix}

Továbbá

R = m g / (4 α)

. A rúd emelkedése ebben az esetben:

\begin{matrix} Δ h = 2 (R β - R sin β) = m g / (2 α) \cdot (β - sin β) . \end{matrix}

Ez a helyzet akkor áll fenn, ha

\begin{matrix} 2 R β \leq L, vagyis m g / (2 α) \cdot β \leq L . \end{matrix}

Ha ez a feltétel nem teljesül, nyilván az i) esetről van szó, így a (6) feltétel ekvivalens a következővel:

\begin{matrix} \frac{m g}{2} arc cos \frac{m g - 2 α l}{m g} > L . \end{matrix}

iii) Legyen most

m g \leq 2 α l

, és a fonalak ne érjenek össze. Ekkor a 4. ábrán látható állapotot kell elemeznünk.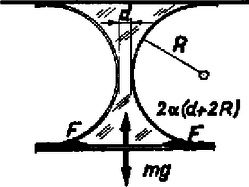

4. ábra

A fonalak hozzásimulnak a rúdhoz, és részben hozzá is tapadnak. A rúdra ható erők függőleges komponenseinek egyensúlyi feltétele:

\begin{matrix} m g = (d + 2 R) \cdot 2 α . \end{matrix}

A fonál hosszára vonatkozó feltétel:

\begin{matrix} L = l - d - 2 R + R π . \end{matrix}

Az egyenletrendszert megoldva:

\begin{matrix} R = \frac{m g + 2 α L - 2 α l}{2 α π} . \end{matrix}

A rúd emelkedése most a következő:

\begin{matrix} Δ h = L - 2 R = \frac{2 α l + α L (π - 2) - m g}{α π} . \end{matrix}

Ez az eset akkor jön létre, ha

d

-re pozitív szám adódik, így a következő feltételt kapjuk:

\begin{matrix} m g / (4 α) \cdot (π - 2) + l > L . \end{matrix}

iv) Most legyen

m g \leq 2 α l

és a fonalak érjenek össze. Az ekkor létrejövő állapotot az 5. ábra mutatja.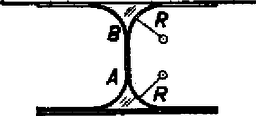

5. ábra

Nyilvánvalóan érvényes a (3) és a (7) egyenlet, amiből

\begin{matrix} R = m g / 4 α . \end{matrix}

A rúd emelkedésére a következőt kapjuk:

\begin{matrix} Δ h = (l - 2 R + R π) - 2 R = l + m g / (4 α) \cdot (π - 4) . \end{matrix}

Ez az állapot akkor jön létre, ha a fonál elég hosszú, azaz a feltétel:

\begin{matrix} m g / (4 α) \cdot (π - 2) + l \leq L . \end{matrix}

Harsányi Gábor (Bp., Radnóti M. Gyak. Gimn., IV. o. t.)

II. megoldás. A fonalak és rudak között maradó folyadékhártya felületi feszültsége csökkenteni igyekszik a folyadékfelszínt. Az egyensúlyi állapotra jellemző, hogy a rendszer potenciális energiája minimális (a helyzet kis megváltoztatása a potenciális energia növekedésével jár együtt). A rendszer helyzeti energiája a folyadék felületi és a rúd helyzeti energiájának összege. Számoljuk ki a 2. ábrán látható elrendezés helyzeti energiáját!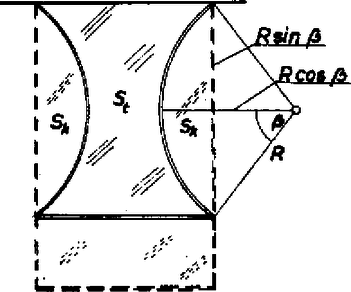

6. ábra

A folyadékhártya felületét a 6. ábra alapján határozhatjuk meg:

\begin{matrix} S = S_{t} - 2 \cdot S_{k} . \end{matrix}

S_{t}

egy téglalap felülete:

S_{t} = 2 \cdot l R sin β

;

S_{k}

egy körszelet,területét egy körcikk és egy háromszög területének különbségeként kapjuk:

S_{k} = R^{2} (β - sin β cos β)

. Felhasználva, hogy

R = L / (2 β)

, kapjuk a folyadékhártya felületi energiáját:

\begin{matrix} W_{f} = 2 α L (l \frac{sin β}{β} - \frac{L}{4} \cdot \frac{2 β - sin 2 β}{β^{2}}) . \end{matrix}

A rúd helyzeti energiája a kezdeti állapothoz viszonyítva:

\begin{matrix} W_{r} = m g (L - 2 R sin β) . \end{matrix}

A teljes energiára így a következő kifejezést kapjuk:

\begin{matrix} W = 2 α L (l \frac{sin β}{β} - \frac{L}{4} \cdot \frac{2 β - sin 2 β}{β^{2}}) + m g L (1 - \frac{sin β}{β}) . \end{matrix}

Számítsuk ki a helyzeti energia

β

szerinti deriváltját:

\begin{matrix} W' (β) = \frac{cos β (β - tg β)}{β^{2}} \cdot L [2 α l - m g + 2 α L \frac{cos β}{β}] . \end{matrix}

Ennek a kifejezésnek a zéróhelye adja az egyensúlyi helyzetet. A szorzat első tényezője 0 és

90^{\circ}

között nem ad megoldást, így a következő egyenletet kapjuk:

\begin{matrix} \frac{cos β}{β} = \frac{m g - 2 α l}{2 α L} . \end{matrix}

Ez ugyanaz az egyenlet, mint amelyet az előző megoldásban írtunk fel.

Zsigmond Géza (Budapest, Fazekas M. Gyak. Gimn., IV. o. t.)