Kezdőlap


Feladat:	1358. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Benkő Tibor , Kriza György , Németh István
Füzet:	1976/november, 180 - 181. oldal		PDF \| MathML
Témakör(ök):	Pontrendszerek mozgásegyenletei, Nyomóerő, kötélerő, Energia homogén gravitációs mezőben, Szélsőérték differenciálszámítással, Függvények grafikus elemzése, Feladat
Hivatkozás(ok):	Feladatok: 1976/április: 1358. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az egyensúly feltétele, hogy az ábrán látható $G$ súlyú testre ható $G$ súlyerő, $K = Q$ nagyságú kötélerő és a karikára merőleges $N$ kényszererő eredője zérus legyen. Ez a feltétel nyilvánvalóan teljesíthető, ha a $G$ súlyú test a karika $A$ , ill. $B$ pontjában van.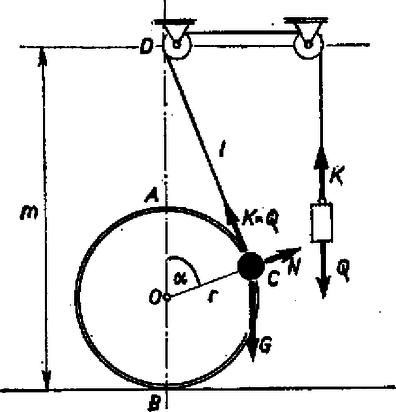

Ha a test az

α

-val jellemezhető

C

pontban van egyensúlyban, a

G

és

Q

erők között a következő összefüggés áll fenn, mivel az erők vektorháromszöge hasonló az

O C D

háromszöghöz:

\begin{matrix} Q / G = l / (m - r), \end{matrix}

(1)

ahol az ábra alapján

\begin{matrix} l = \sqrt[]{{(m - r)}^{2} + r^{2} - 2 r (m - r) cos α} . \end{matrix}

(2)

Az előző két kifejezésből a

cos α

értéke a rendszer egyensúlya esetén:

\begin{matrix} cos α = \frac{{(m - r)}^{2} [1 - Q^{2} / G^{2}] + r^{2}}{2 r (m - r)} . \end{matrix}

(3)

(3) jobb oldala akkor lesz

- 1

és

1

közötti szám, ha

\begin{matrix} m G > (m - r) Q . \end{matrix}

Ezen feltétel teljesülése esetén lehet a szóban forgó egyensúlyi helyzetet megvalósítani.
A feladat szimmetriája miatt az egyensúly feltétele teljesül az

A B

tengely másik oldalán is, így a test a karika négy pontjában lehet egyensúlyban. Ha

Q ≫ G

, akkor az

A

pont stabil, a másik kettő instabil, ellenben, ha

G ≫ Q

, akkor csak a

B

pont lesz stabil. A probléma részletesebb elemzéséhez már a differenciálszámítás ismerete szükséges.
Az egyensúlyi helyzetek stabilitásának vizsgálatánál azt kell megnézni, hogy a testet kimozdítva a vizsgált pontból, a végzett munka pozitív (stabil) vagy negatív-e (instabil állapot). Mivel a külső munka a test helyzeti energiáját változtatja meg, ezért elég azt megnézni, hogy a helyzeti energiának az adott pontban minimuma (stabil) vagy maximuma (instabil) van.
A rendszer helyzeti energiája az

A

pontbeli helyzethez viszonyítva

α

szög függvényében:

\begin{matrix} E (α) = - G r (1 - cos α) + Q [\sqrt[]{{(m - r)}^{2} + r^{2} - 2 r (m - r) cos α} - m + 2 r] . \end{matrix}

(4)

Ezen függvény ismeretében az egyensúlyi helyzeteket a

d E / d α = 0

feltételből is meghatározhattuk volna. Az

E (α)

függvény minimumát, ill. maximumát az egyensúlyi helyzetekben a

d^{2} E / d α^{2}

függvény előjele dönti el. Az

E (α)

függvény második deriváltja:

\begin{matrix} \frac{d^{2} E}{d α^{2}} = [Q \end{matrix}

(5)

Ez a mennyiség az

α = 0

egyensúlyi helyzetben pozitív, azaz az egyensúlyi helyzet stabil, ha

G < [(m - r) / (m - 2 r)] Q

. A

B

pont akkor stabil, ha

G > [(m - r) / m] Q

. A

C

pont mindig instabil, mivel az (5) egyenlet első tagja abban a pontban (1) alapján zérus, a második pedig mindig negatív.
Érdemes megjegyezni, hogy ha

(m - r) / m < G / Q < (m - r) / (m - 2 r)

, akkor mind az

A

, mind a

B

helyzet stabil.

Molnár László