Kezdőlap


Feladat:	1336. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bányász I. , Beke E. , Császár A. , Horváth Gy. , Kalcsú Z. , Kisvárdai L. , Köteles Z. , Nagy Győző , Sallai Á. , Vas Zs.
Füzet:	1976/szeptember, 35 - 38. oldal		PDF \| MathML
Témakör(ök):	Körmozgás (Tömegpont mozgásegyenlete), Newton-féle gravitációs erő, Bolygómozgás, Kepler törvények, Rugalmas erő, Rezgések összetevése (különböző irányokban), Feladat
Hivatkozás(ok):	Feladatok: 1976/január: 1336. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Vizsgáljuk egy ellipszispályán haladó tömegpont mozgását. A rá ható erő a pálya minden pontjában felbontható érintőleges és erre merőleges összetevőre. Ha a vizsgált pontban a görbületi sugár $ϱ$ , a kerületi sebesség pedig $v$ , az erő pályára merőleges összetevője

\begin{matrix} F_{⊥} = m v^{2} / ϱ . \end{matrix}

(1)

Tekintsünk egy olyan ,,bolygómozgást'', ahol az

F_{1}

fókuszpontba helyezett

M

tömegű nap gravitációs terében a

m

tömegű bolygó a megfelelő ellipszispályát írja le.
A

m

tömegű test teljes energiája egy

P

pontban:

\begin{matrix} E = (1 / 2) m v^{2} - γ m M / r_{1} = - γ m M / a, \end{matrix}

(2)

ahol

r_{1} = F_{1} P

a

a fél nagytengely. Innen

\begin{matrix} m v^{2} = γ m M [(2 / r_{1}) - (1 / a)] . \end{matrix}

(3)

A gravitációs erőnek a pillanatnyi sebességre merőleges összetevője:

\begin{matrix} F_{⊥} = (γ m M / r_{1}^{2}) cos α, \end{matrix}

(4)

ahol

α

r_{1}

vezérsugár és az érintő által bezárt szög pótszöge (1. ábra).

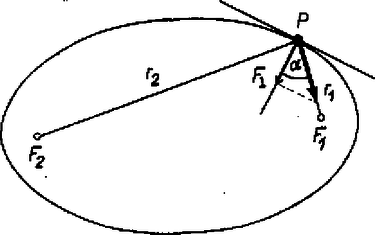1. ábra

Az (1) ‐ (4) egyenletekből

\begin{matrix} ϱ = m v^{2} / F_{⊥} = (r_{1}^{2} / cos α) [(2 / r_{1}) - (1 / a)], \end{matrix}

illetve felhasználva a másik vezérsugárra vonatkozó

r_{2} = 2 a - r_{1}

összefüggést:

\begin{matrix} ϱ = r_{1} r_{2} / (a cos α) . \end{matrix}

(5)

cos α

meghatározását tekinthetjük geometriai feladatnak, de továbbhaladhatunk ,,tisztán'' fizikai úton is ‐ a Kepler-törvények segítségével. Kepler II. törvénye értelmében a területi sebesség állandó:

\begin{matrix} (1 / 2) r_{1} v cos α = áll. = c . \end{matrix}

(6)

T

keringési idő alatt a rádiuszvektor az egész ellipszis területét végigpásztázza, azaz

\begin{matrix} c T = a b π . \end{matrix}

(7)

Kepler III. törvénye szerint a keringési idő csak a fél nagytengelytől függ, tehát egy

a

sugarú körpályán mozgó test keringési ideje is

T

. Körpályára:

\begin{matrix} γ m M / a^{2} = m {(\frac{2 π a}{T})}^{2} / a . \end{matrix}

(8)

(6), (7) és (8)-ból

T

kiküszöbölésével a

\begin{matrix} γ M / r_{1}^{2} = (a v^{2} / b^{2}) cos^{2} α \end{matrix}

(9)

egyenlethez jutunk, azaz

\begin{matrix} F_{⊥} = (γ m M / r_{1}^{2}) cos α = m v^{2} (a / b^{2}) cos^{3} α, \\ ϱ = m v^{2} / F_{⊥} = b^{2} / (a cos^{3} α) . & (10) \end{matrix}

A Kepler-törvények segítségével ‐ más úton ‐ ismét meghatároztuk a görbületi sugarat.
Az (5) és (10) eredmények ismeretében

cos α

geometriai meghatározására már nincs szükség. A kétismeretlenes egyenletrendszert

ϱ

-ra megoldva végeredményül a

\begin{matrix} ϱ = \frac{{(r_{1} r_{2})}^{3 / 2}}{a b} \end{matrix}

(11)

görbületi sugarat kapjuk.

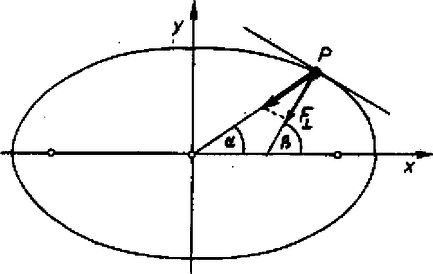2. ábra

A 2. ábrán látható koordináta-rendszert használva kapjuk:

\begin{matrix} r_{1}^{2} = {(c - x)}^{2} + y^{2}, r_{2}^{2} = {(c + x)}^{2} + y^{2}, \end{matrix}

így az

a^{2} - b^{2} + c^{2}

azonosság alapján

\begin{matrix} ϱ = a^{2} b^{2} {(\frac{x^{2}}{a^{4}} + \frac{y^{2}}{b^{4}})}^{3 / 2} . \end{matrix}

(12)

A kérdezett pontokban

ϱ

rendre

3, 6 cm

16, 6 cm

, illetve

9, 5 cm

II. megoldás. Vizsgáljuk egy

D

direkciós erejű rugó végére kötött

m

tömegű test síkmozgását.
A Newton egyenletet derékszögű koordináta-rendszerben felírva (a mennyiségek fölé írt két pont az idő szerinti második differenciálhányadost jelenti):

\begin{matrix} F_{x} = - D x = m \ddot{x}, \\ F_{y} = - D y = m \ddot{y} . & (1) \end{matrix}

Ezeknek az egyenleteknek van olyan

\begin{matrix} x = a sin ω t, \\ y = b cos ω t, (ω = \sqrt[]{D / m}) & (2) \end{matrix}

megoldása, amely a kívánt ellipszispályát írja le:

\begin{matrix} x^{2} / a^{2} + y^{2} / b^{2} = sin^{2} ω t + cos^{2} ω t = 1. \end{matrix}

Tehát megfelelő kezdőpontot és kezdeti sebességet választva az

m

tömegű test a megadott ellipszispályán fog mozogni.
A sebességkomponensek:

\begin{matrix} v_{x} = a ω cos ω t, \\ v_{y} = - b ω sin ω t . & (3) \end{matrix}

(x, y)

pontban az érintő iránytangense:

\begin{matrix} m = v_{y} / v_{x} = - (b / a) (sin ω t / cos ω t) = - (b^{2} / a^{2}) (x / y), \end{matrix}

az erre merőleges egyenes iránytangense a 2. ábra alapján:

\begin{matrix} m' = - (1 / m) = (a^{2} / b^{2}) (y / x) = tgβ. \end{matrix}

(4)

A rugóerő pályára merőleges komponense a 2. ábra alapján

\begin{matrix} F_{⊥} = F cos (α - β) = D \sqrt[]{x^{2} + y^{2}} cos (α - β), \end{matrix}

(5)

ahol

\begin{matrix} tgα=y/x. \end{matrix}

(6)

A szögfüggvényekre vonatkozó azonosságok felhasználásával

\begin{matrix} cos (α - β) = {[(x^{2} + y^{2}) (x^{2} / a^{4} + y^{2} / b^{4})]}^{- 1 / 2}, \end{matrix}

azaz

\begin{matrix} F_{⊥} = \frac{D}{\sqrt[]{\frac{x^{2}}{a^{4}} + \frac{y^{2}}{b^{4}}}} . \end{matrix}

(7)

A görbületi sugár meghatározásához még szükség van a sebesség négyzetére. (3)-ból

\begin{matrix} v^{2} = ω^{2} (a^{2} cos^{2} ω t + b^{2} sin^{2} ω t) = ω^{2} a^{2} b^{2} [(x^{2} / a^{4}) + (y^{2} / b^{4})] . \end{matrix}

(8)

A görbületi sugár tehát az ellipszis

(x, y)

pontjában:

\begin{matrix} ϱ = \frac{m v^{2}}{F_{⊥}} = \frac{m ω^{2}}{D} a^{2} b^{2} {(\frac{x^{2}}{a^{4}} + \frac{y^{2}}{b^{4}})}^{3 / 2} = a^{2} b^{2} {(\frac{x^{2}}{a^{4}} + \frac{y^{2}}{b^{4}})}^{3 / 2} . \end{matrix}

(9)

Nagy Győző (Jászberény, Lehel Vezér Gimn., II. o. t.)