Kezdőlap


Feladat:	1294. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Szathmári Attila , Zelhofer Walter
Füzet:	1976/február, 89 - 92. oldal		PDF \| MathML
Témakör(ök):	Tökéletesen rugalmas ütközések, Newton-féle gravitációs erő, Kepler I. törvénye, Kepler II. törvénye, Meteorok, Mesterséges holdak, Feladat
Hivatkozás(ok):	Feladatok: 1975/május: 1294. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Centrális térben történő mozgáskor az energia és az impulzusmomentum mozgásállandó. A Föld gravitációs terében haladó $m$ tömegű, $v$ sebességű űrhajó teljes energiája

\begin{matrix} (1 / 2) m v^{2} - f M m / r = E, \end{matrix}

(1)

impulzusmomentuma:

\begin{matrix} m r v sin φ = N, \end{matrix}

(2)

ahol

φ

az r helyvektor és a v sebességvektor által bezárt szög.
Kezdeti feltételként ismerve a teljes energiát és az impulzusmomentumot, (1) és (2) segítségével meghatározható a pálya alakja, a hely és a sebesség minden időpontban. Zárt pálya esetén a Kepler‐törvények is közvetlenül adódnak a megoldásból.
A rövidség kedvéért tekintsük ismertnek Kepler I. törvényét, azaz hogy ha

E < 0

, az űrhajó pályája ellipszis (1. ábra).

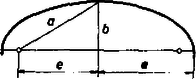1. ábra

Az (1) és (2) összefüggést csupán az ellipszispálya adatainak meghatározására használjuk fel.

Ha az űrhajó sebessége Földközelben

v_{max}

, a legtávolabbi pontban

v_{min}

, a teljes energia ebben a két pontban:

\begin{matrix} E = \frac{1}{2} m v_{max}^{2} - \frac{f M m}{a - e} = \frac{1}{2} m v_{min}^{2} - \frac{f M m}{a + e} . \end{matrix}

(3)

Mivel a két szélső esetben

v ⊥ r

, ezekben a pontokban az impulzusmomentum:

\begin{matrix} N = m (a - e) v_{max} = m (a + e) v_{min}, \end{matrix}

(4)

A (3) és (4) egyenleteket

v_{max}

-ra megoldva:

\begin{matrix} \frac{1}{2} m v_{max}^{2} = \frac{f M m}{2 a} - \frac{a + e}{a - e}, \end{matrix}

(5)

amit (3)-ba visszahelyettesítve a teljes energia:

\begin{matrix} E = - f M m / 2 a . \end{matrix}

(6)

Ez az egyenlet ‐ azon a felismerésen túl, hogy a teljes energia a pálya adatai közül csupán a nagytengelytől függ ‐ az (1) egyenletbe téve fontos összefüggést jelent:

\begin{matrix} \frac{1}{2} m v^{2} - \frac{f M m}{r} = - \frac{f M m}{2 a}, \end{matrix}

(7)

vagy átrendezve:

\begin{matrix} v^{2} = f M (\frac{2}{r} - \frac{1}{a}), \end{matrix}

(8)

Az indítási pontban

r_{0} = 2 \cdot 10^{7} m

v_{0} = 6 \cdot 10^{3} m/s

, és így (8) segítségével a fél nagytengely:

\begin{matrix} a = \frac{f M r_{0}}{2 f M - r_{0} v_{0}^{2}} = 10 \cdot 10^{7} m . \end{matrix}

(9)

Mivel

\begin{matrix} r_{0} = a - e, illetve e = 8 \cdot 10^{7} m, & (10) \\ b = \sqrt[]{a^{2} - e^{2}} = 6 \cdot 10^{7} m . & (11) \end{matrix}

(8) alapján a kistengely végpontjában (ahol

r = a

) az űrhajó sebessége

\begin{matrix} v_{1} = \sqrt[]{f M (\frac{2}{a} - \frac{1}{a})} = 2 \cdot 10^{3} m/s . \end{matrix}

(12)

m_{1}

tömegű űrhajó

v_{1} = 2 \cdot 10^{3} m/s

sebességgel halad, amikor az

m_{2}

tömegű,

v_{2} = - 0, 5 \cdot 10^{3} m/s

sebességű meteorral ütközik. Centrális, rugalmas ütközést feltételezve, az ütközés utáni sebességek:

\begin{matrix} u_{1} & = 2 \frac{m_{1} v_{1} + m_{2} v_{2}}{m_{1} + m_{2}} - v_{1} = + 0, 75 \cdot 10^{3} m/s, & (13) \\ u_{2} & = 2 \frac{m_{1} v_{1} + m_{2} v_{2}}{m_{1} + m_{2}} - v_{2} = + 3, 25 \cdot 10^{3} m/s . & (14) \end{matrix}

(Pozitív iránynak az űrhajó ütközés előtti sebességét választottuk.)
Az űrhajó sebessége ‐ így energiája is ‐ csökken, továbbra is ellipszisszis pályán halad. Az új pálya fél nagytengelye

α'

, (8) alapján

\begin{matrix} u_{1}^{2} = f M [(2 / a) - (1 / a')], \end{matrix}

(15)

ahonnan

\begin{matrix} a' = 5, 38 \cdot 10^{7} m . \end{matrix}

(16)

A sebesség irányának egyenese mindig a pálya érintője. Mivel centrális ütközésnél ezen egyenes iránya nem változik, az eredeti és az új pálya az ütközési pontban közös érintővel rendelkezik (2. ábra).

2. ábra

Az érintőszerkesztés szabályai szerint az új ellipszispálya második fókusza az eredeti ellipszis második fókuszához vezető vezérsugáron van.
Az új pálya

e'

excentricitásának,

b'

fél kistengelyének meghatározása ‐ a 2. ábra alapján ‐ egyszerű geometriai feladat. Az ellipszis mértani hely tulajdonságát felhasználva

\begin{matrix} A C + C B' = 2 a', \end{matrix}

(17)

másrészt ismerjük az

\begin{matrix} A C = a, A B' = 2 e', A B = 2 e \end{matrix}

(18)

távolságokat. A cosinus tételt alkalmazva az

A B C

, illetve az

A B' C

háromszögekre:

\begin{matrix} {(2 e)}^{2} = a^{2} + a^{2} - 2 a \end{matrix}