Kezdőlap


Feladat:	1293. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Faragó Béla , Kisvárdai László , Vancsó Ödön
Füzet:	1976/február, 87 - 89. oldal		PDF \| MathML
Témakör(ök):	Pontrendszerek mozgásegyenletei, Newton-féle gravitációs erő, Körmozgás (Tömegpont mozgásegyenlete), Egyéb a Hold mozgásával kapcsolatos jelenségek, A Föld forgása, Szinkron-műhold (szinkronpálya), Feladat
Hivatkozás(ok):	Feladatok: 1975/május: 1293. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Olyan mesterséges égitestet akarunk létrehozni, mely a Holdnak ugyanazon pontja fölött található. Mivel a Holdnak mindig ugyanaz az oldala fordul a Föld felé, ez csak úgy lehetséges, hogy a mesterséges égitest egy olyan mesterséges hold, amely a Hold pályasíkjában, a Holdéval megegyező szögsebességel kering a Föld körül.

A Föld‐Hold rendszer tömegközéppontja közel esik a Föld középpontjához, így nem követünk el nagy hibát, ha úgy számolunk, mintha a Hold az álló Föld középpontja körül körpályán keringene. A mesterséges égitestet csak a Föld és a Hold középpontját összekötő centrálison helyezhetjük el, mivel a rá ható erők eredőjének a Föld középpontja felé kell mutatnia. Három helyzet lehetséges (1‐3. ábra).

a) Az

m

tömegű mesterséges hold a Föld és a Hold között, a Földtől

x

távolságra helyezkedik el (1. ábra).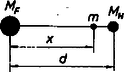

1. ábra

A körmozgáshoz szükséges centripetális erőt a Föld és a Hold vonzóerejének eredője biztosítja:

\begin{matrix} f \frac{M_{F} m}{x^{2}} - f \frac{M_{H} m}{{(d - x)}^{2}} = m x ω^{2} . \end{matrix}

(1)

ω

megegyezik a Hold szögsebességével, így a Holdra vonatkozó hasonló egyenletből határozható meg:

\begin{matrix} f \frac{M_{F} M_{H}}{d^{2}} = M_{H} d ω^{2} . \end{matrix}

(2)

A két egyenletből

ω

-t kiküszöbölve

\begin{matrix} \frac{M_{F}}{x^{3}} - \frac{M_{H}}{{(d - x)}^{2} x} = \frac{M_{F}}{d^{3}}, \end{matrix}

M_{F} / M_{H} = c \approx 81, 3

és

x / d = α

helyettesítéssel

\begin{matrix} c - {(\frac{α}{1 - α})}^{2} = c α^{3} . \end{matrix}

(3)

Ennek az egyenletnek 0 és 1 közé eső gyökét valamilyen közelítő módszerrel kereshetjük meg.

c

numerikus értékét behelyettesítve (3)-at így is írhatjuk:

\begin{matrix} 81, 3 = 81, 3 α^{3} + {[\frac{1}{1 - α} - 1]}^{2} . \end{matrix}

Ennek az egyenletnek a jobb oldalán álló kifejezés a

[0, 1)

intervallumban

α

-nak szigorúan monoton növekedő függvénye, a függvény értéke

α = 0

esetén 0,

α = 1

-ben a baloldali határértéke pedig

+ \infty

. Ezért a szóbanforgó folytonos függvény a

[0, 1)

intervallumban pontosan egy helyen felveszi a

81, 3

értéket, azaz a fenti egyenletnek pontosan egy gyöke van a

[0, 1)

intervallumban. Közelítő számítással a gyökre

α \approx 0, 849

adódik, tehát a mesterséges égitest a Föld középpontjától

3, 27 \cdot 10^{5} km

, a Hold középpontjától

0, 58 \cdot 10^{5} km

távolságra kering.

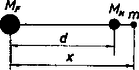2. ábra

b) Ha a mesterséges hold a Hold túlsó oldalán van (2. ábra), az (1) egyenlet a következő alakot ölti:

\begin{matrix} f \frac{M_{F} m}{x^{2}} + f \frac{M_{H} m}{{(x - d)}^{2}} = m x ω^{2} . \end{matrix}

(4)

(2) felhasználásával és az előbbi helyettesítésével

\begin{matrix} c + {(\frac{α}{α - 1})}^{2} = c α^{3} \end{matrix}

(5)

egyenlet adódik, amelynek 1-nél nagyobb megoldása

α \approx 1, 168

. (Az a tény, hogy (5)-nek pontosan egy 1-nél nagyobb gyöke van, (5) alábbi alakjából következik a fentiekhez hasonló módon:

\begin{matrix} \frac{81, 3}{α^{3}} + \frac{1}{α {(α - 1)}^{2}} = 81, 3. \end{matrix}

Tehát a szinkron mesterséges hold a Hold túlsó oldalára a Földtől

4, 50 \cdot 10^{5}

km, a Holdtól

0, 65 \cdot 10^{5}

km távolságra is elhelyezhető.

c) A mesterséges hold elvileg elhelyezhető a Földnek a Holddal átellenes oldalán is (3. ábra).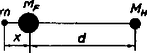

3. ábra

Ekkor

\begin{matrix} f \frac{M_{F} m}{x^{2}} + f \frac{M_{H} m}{{(d + x)}^{2}} = m x ω^{2}, \end{matrix}

(6)

ahonnan (2) felhasználásával

\begin{matrix} c + {(\frac{α}{α + 1})}^{2} = c α^{3} . \end{matrix}

(7)

Megoldva az egyenletet,

α \approx 1, 001

, adódik, tehát a Hold hatása gyakorlatilag elhanyagolható, a mesterséges hold a Holdénál alig nagyobb sugarú pályán kering.

Vancsó Ödön (Gödöllő, Török I. Gimn., III. o. t.) dolgozata alapján

Megjegyzések. 1. Vizsgáljuk meg, mennyire változtatja meg az eredményeket, ha figyelembe vesszük, hogy a Hold és a mesterséges hold nem a Föld középpontja, hanem a Föld‐Hold rendszer tömegközéppontja körül kering (a mesterséges hold tömege a Föld és a Hold tömegéhez képest elhanyagolható).

Legyen a tömegközéppont

r

távolságra a Föld középpontjától. Ekkor

\begin{matrix} M_{F} / M_{H} = (d - r) / r, \end{matrix}

(8)

ahonnan

\begin{matrix} β = r / d = 1 / (1 + c) . \end{matrix}

(9)

Vizsgáljuk meg pl. azt az esetet, amikor a mesterséges hold a Föld és a Hold között helyezkedik el (4. ábra).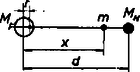

4. ábra

Ekkor az (1)-nek és (2)-nek megfelelő egyenletek

\begin{matrix} f \frac{M_{F} m}{x^{2}} - f \frac{M_{H} m}{{(d - x)}^{2}} = m (x - r) ω^{2}, & (10) \\ f \frac{M_{F} M_{H}}{d^{2}} = M_{H} (d - r) ω^{2} . & (11) \end{matrix}

ω

-t kiküszöbölve

α = x / d

-re az alábbi egyenlet adódik:

\begin{matrix} c (\frac{α}{α - β}) - {(\frac{α}{1 - α})}^{2} \cdot (\frac{α}{α - β}) = c α^{2} \frac{α}{1 - β}, \end{matrix}

(12)

amelynek megoldása ‐

α \approx 0, 851

‐ alig tér el az

r

elhanyagolásával kapott

α \approx 0, 849

értéktől. A másik két helyzetben az eltérés még kisebb.

Kisvárdai László József (Csongrád, Batsányi J. Gimn., II. o. t.) dolgozata alapján

2. Ha figyelembe vesszük, hogy a mesterséges égitest nem a Föld, hanem a középpontjától

r

távolságra levő tömegközéppont körül kering, akkor a gravitációs erők eredője akkor is mutathat a középpont felé, ha a Föld, a Hold és a mesterséges hold nem esik egy egyenesbe (5. ábra).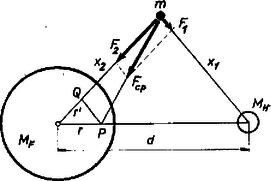

5. ábra

Legyen

P Q

párhuzamos a Holdat a mesterséges égitesttel összekötő egyenessel. Ekkor

\begin{matrix} r' / r = x_{2} / d, \end{matrix}

(13)

r = d / (1 + c)

felhasználásával

\begin{matrix} r' = x_{2} / (1 + c) . \end{matrix}

(14)

Háromszögek hasonlóságából

\begin{matrix} \frac{F_{2}}{F c p} = \frac{x_{2} - r'}{x} . \end{matrix}

(15)

F_{2} = f M_{F} m / x_{2}^{2}

F_{c p} = m x ω^{2}

, így (15)-ből (14)-et is felhasználva

\begin{matrix} \frac{f \frac{M_{F} m}{x_{2}^{2}}}{m x ω^{2}} = \frac{x_{2} - \frac{x_{2}}{1 + c}}{x}, ahonnan \\ x_{2}^{3} = \frac{f M_{F} (1 + c)}{c ω^{2}} . \end{matrix}

ω

-t (11)-ből behelyettesítve

\begin{matrix} x_{2} = d \end{matrix}

adódik. Hasonlóan belátható, hogy

x_{1} = d

, vagyis a mesterséges hold úgy is elhelyezhető a Hold pályasíkjában, hogy a Földdel és a Holddal egyenlő oldalú háromszöget alkosson. Természetesen két ilyen helyzet lehetséges.

Faragó Béla (Csongrád, Batsányi J. Gimn., III. o. t.) dolgozata alapján