Kezdőlap


Feladat:	1210. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ábrahám Tibor
Füzet:	1975/február, 87 - 89. oldal		PDF \| MathML
Témakör(ök):	Egyéb kényszermozgás, Körmozgás (Tömegpont mozgásegyenlete), Newton-féle gravitációs erő, Kepler III. törvénye, Rezgőmozgás (Tömegpont mozgásegyenlete), Feladat
Hivatkozás(ok):	Feladatok: 1974/április: 1210. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az ellipszispályát a kérdéses pontokban helyettesíthetjük a megfelelő görbületi körökkel. Ekkor az ellipszispályán való tartáshoz

\begin{matrix} F'_{m} = m \cdot v^{2} / ϱ \end{matrix}

(1)

nagyságú erő szükséges, ahol

ϱ

a görbületi sugár. A görbületi sugár meghatározása általában differenciálgeometriai úton történhet, ez azonban magasabb matematikai ismereteket igényel.
A probléma megoldható elemi módszerekkel is. A falra ható erő egy bizonyos pontban (1) alapján csak a pillanatnyi sebességtől függ, a golyó mozgása tehát helyettesíthető egy olyan ellipszispályán történő változó sebességű mozgással, amelynek az adott pontban a golyó sebességével azonos a sebessége. Ilyen mozgás lehet például a bolygómozgás.
Helyezzünk az ellipszis egyik gyújtópontjába egy olyan testet, amely a golyóra

F = k / r^{2}

nagyságú vonzóerővel hat.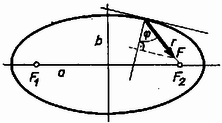

1. ábra

Az 1. ábra alapján a pálya egy

P

pontjában a kényszerpályát helyettesítő "műnap''

\begin{matrix} F_{m} = F \cdot cos φ \end{matrix}

(2)

nagyságú pályára merőleges erőt fejt ki. A bolygómozgás és a kényszermozgás egyenértékűségét a

P

pontban

k

alkalmas megválasztásával érhetjük el.
Kepler II. törvénye szerint a területi sebesség állandó:

\begin{matrix} (1 / 2) r \cdot v cos φ = áll . \end{matrix}

T

keringési idő alatt a vezérsugár az egész

a b π

területet súrolja, tehát

\begin{matrix} (1 / 2) r \cdot v \cdot (cos φ) \cdot T = a b π : \end{matrix}

(3)

A keringési időt Kepler III. törvényének felhasználásával határozhatjuk meg. Vegyünk egy

a

sugarú körpályát, melynek középpontjában ugyanaz a "műnap'' van. Ekkor a körpályán keringő bolygónak szintén

T

a keringési ideje. Newton II. törvénye szerint

F = m v^{2} / a

, azaz

\begin{matrix} \frac{k}{a^{2}} = \frac{m}{a} {(\frac{2 a π}{T})}^{2} . \end{matrix}

(4)

Ebből

\begin{matrix} T = 2 a π \sqrt[]{\frac{m a}{k}}, \end{matrix}

(5)

amit a (3) egyenletbe helyettesítve,

k

-ra a következőt kapjuk:

\begin{matrix} k = m \cdot (a / b^{2}) {(r \cdot v \cdot cos φ)}^{2} . \end{matrix}

(6)

Itt

v

az eredeti mozgás sebessége (ez állandó, mert nincs súrlódás), ami a

φ

szöggel jellemzett helyen éppen megegyezik a

k

állandóval megadott bolygómozgás pillanatnyi sebességével. A kapott összefüggés alapján a (2) egyenletből

F_{m}

meghatározható:

\begin{matrix} F_{m} = m v^{2} (a / b^{2}) cos^{3} φ . \end{matrix}

(7)

A kérdéses három pontban ható kényszererők nagyságát

cos φ

ismeretében számíthatjuk ki (2. ábra).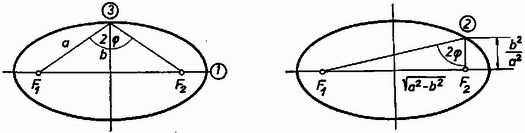

2. ábra

1. Látható, hogy

φ = 0

;

cos φ = 1

, tehát

\begin{matrix} F_{1} = m v^{2} \cdot a / b^{2} = 78, 1 N . \end{matrix}

2. Felhasználjuk, hogy az ellipszis vezérsugarai az érintővel azonos szöget zárnak be, tehát a vezérsugarak közötti szögfelező merőleges az érintőre.
A 2. ábra alapján

\begin{matrix} cos 2 φ = \frac{\bar{F 2}}{\bar{F' 2}} = \frac{b^{2} / a}{(2 a^{2} - b^{2}) / a} = \frac{b^{2}}{2 a^{2} - b^{2}}, \\ cos φ = \sqrt[]{\frac{a^{2}}{2 a^{2} - b^{2}}} . \end{matrix}

Ezt a (7) egyenletbe helyettesítve:

\begin{matrix} F_{2} = m v^{2} \frac{a^{4}}{b^{2} {(2 a^{2} - b^{2})}^{3 / 2}} = 49, 3 N . \end{matrix}

cos φ

értékét azonnal felírhatjuk:

cos φ = b / a

, így

\begin{matrix} F_{3} = m v^{2} \cdot b / a^{2} = 40, 1 N . \end{matrix}

Ábrahám Tibor (Eger, Gárdonyi G. Gimn.. IV. o. t.)

Megjegyzés. A feladat megoldható úgy is, hogy az ellipszis‐mozgást egy, az ellipszis középpontjába helyezett rugó segítségével hozzuk létra. Ezzel a módszerrel nem érkezett helyes megoldás, mert a megoldók nem gondoltak arra, hogy a rugóerőnek csak a pályára merőleges komponense számít.