Kezdőlap


Feladat:	1172. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Major János
Füzet:	1974/szeptember, 37 - 40. oldal		PDF \| MathML
Témakör(ök):	Hajítások, Egyéb merev test kinematika, Feladat
Hivatkozás(ok):	Feladatok: 1973/december: 1172. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Koordináta-rendszerünk kezdőpontja legyen a labdát dobó játékos lábánál, az $x$ tengely vízszintes, az $y$ -tengely pedig függőleges.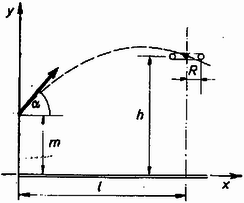

A hajítási pályát leíró egyenletrendszer (

v_{0}

a kezdősebesség):

\begin{matrix} x & = v_{0} \cdot t \cdot cos α, & (1) \\ y & = m + v_{0} \cdot t \cdot sin α - (1 / 2) g t^{2}; & (2) \end{matrix}

illetve a sebesség vizszintes és függőleges komponense:

\begin{matrix} v_{x} & = v_{0} cos α, & (3) \\ v_{y} & = v_{0} sin α - g \cdot t . & (4) \end{matrix}

Az (1) egyenletből a

t

időt kifejezve és behelyettesítve megkapjuk a pálya egyenletét:

\begin{matrix} y = m + x tg α - [g x^{2} / (2 v_{0}^{2})] (1 + {tg}^{2} α) . \end{matrix}

(5)

Először tegyük fel, hogy a labda pontszerű. A kosárnak a dobás síkjában levő két pontja:

(l - R; h)

és

(l + R; h)

. A labda felülről érkezik a kosárba, azaz az

(l - R; h)

pont felett, és az

(l + R, h)

pont alatt kell elhaladnia:

\begin{matrix} h < m + (l - R) tg α - \frac{g {(l - R)}^{2}}{2 v_{0}^{2}} (1 + {tg}^{2} α), \end{matrix}

(6)

és

\begin{matrix} h > m + (l + R) tg α - \frac{g {(l + R)}^{2}}{2 v_{0}^{2}} (1 + {tg}^{2} α), \end{matrix}

(7)

Ez a két egyenlőtlenség határozza meg, hogy milyen

v_{0}

és

α

értékek mellet lehet a kosárba beletalálni.
A (6) és (7) egyenlőtlenség a következő egyenlőtlenségekkel ekvivalens:

\begin{matrix} (l - R) tg α - (h - m) > 0, & (8) \\ \frac{(g / 2) {(l - R)}^{2} (1 + {tg}^{2} α)}{(l - R) tg α - (h - m)} < v_{0}^{2} < \frac{(g / 2) {(l + R)}^{2} (1 + {tg}^{2} α)}{(l + R) tg α - (h - m)} . & (9) \end{matrix}

Ezért szükséges, hogy (9) bal oldala kisebb legyen a jobb oldalnál, ebből a hajítás szögére kapjuk az alábbi szükséges feltételt:

\begin{matrix} tg α > \frac{2 l (h - m)}{l^{2} - R^{2}} . \end{matrix}

(10)

Másrészt amennyiben

α

kielégíti ezt a feltételt, akkor meg lehet választani a

v_{0}

kezdősebességet úgy, hogy a pontszerű labda ,,csont nélkül'' essék a kosárba. Ugyanis (10)-ből következik, hogy (9) bal oldala kisebb, mint a jobb oldal, így ekkor van olyan

v_{0}

sebesség, amely kielégíti a (9) feltételt. Ilyen sebesség mellett a labda ,,csont nélkül'' esik a kosárba, hiszen a (8) feltétel is következik a (10) egyenlőtlenségből.
Mivel a tangens függvény monoton növekvő, a dobási szög nagyobb kell, hogy legyen

α_{min}

értéknél, ahol

\begin{matrix} tg α_{min} = \frac{2 l (h - m)}{l^{2} - R^{2}} . \end{matrix}

A terem magasságának meghatározásához a pálya legmagasabb pontjának koordinátáit kell kiszámítani a legkedvezőbb

α = α_{min}

határesetben. A függőleges sebességkomponens a legmagasabb pontban nulla, azaz (4)-ből

\begin{matrix} t = (v_{0} / g) sin α_{min}, \end{matrix}

(11)

amit (2)-be helyettesítve kapjuk, hogy a terem magasságának nagyobbnak kell lennie, mint

\begin{matrix} H_{min} = \frac{h l^{2} - m R^{2}}{l^{2} - R^{2}} \end{matrix}

(12)

(ez a kifejezés nagyobb

h

-nál, mivel

m < h

).
Vizsgáljuk meg azt az esetet, amikor a labda sugara

r

. A legegyszerűbben úgy vehetjük figyelembe a labda kiterjedését, hogy továbbra is pontszerű labdát véve, a labda pályasíkjában a kosár két szélső pontját

r

sugarú körökkel helyettesítjük. Könnyen felírhatjuk a két kör egyenletét, és a hajítási szög és sebesség értéke határesetben olyan lesz, amelynél az (5) parabola mindkét kört érinti. A kapott negyedfokú egyenletrendszert azonban egzakt módszerrel nem tudjuk megoldani. Ezért feltételezve, hogy

l ≫ R

, és hogy

R

és

r

között nincs nagyságrendi különbség, közelítő megoldást keresünk. Ilyen feltételek mellett a labda pályája a kosárba esés pillanatában egyenessel közelíthető, amelynek vízszintessel bezárt szöge legyen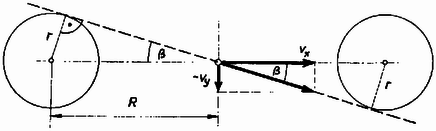

β

Az ábra alapján

\begin{matrix} tg β = \frac{r}{\sqrt[]{R^{2} - r^{2}}}, \end{matrix}

(13)

de másképpen (3) és (4) szerint, az időt ismét (1) segítségével kiküszöbölve, feltételezve, hogy a labda koordinátája

(l; h)

\begin{matrix} tg β = \frac{- v_{y}}{v_{x}} = \frac{g \cdot l}{v_{0}^{2}} (1 + {tg}^{2} α) - tg α . \end{matrix}

(14)

(13)-ból és (14)-ből, továbbá az (5) pályaegyenletből megkapjuk a minimális hajítási szöget, amely a ,,csont nélküli'' találat határesetéhez tartozik:

\begin{matrix} tg α_{min} = 2 \frac{h - m}{l} + \frac{r}{\sqrt[]{R^{2} - r^{2}}}, \end{matrix}

(15)

és a szükséges terem magasság a parabola csúcsmagasságának és a labda sugarának összege:

\begin{matrix} H_{min} = m + \frac{{((h - m) + \frac{l r}{2 \sqrt[]{R^{2} - r^{2}}})}^{2}}{(h - m) + \frac{l r}{\sqrt[]{R^{2} + r^{2}}}} + r . \end{matrix}

(16)

Számolásunk közelítő, így nem csodálkozhatunk, hogy (15)-be

r = 0

-t helyettesítve, nem kapjuk meg a (10) egzakt eredményt.

Megjegyzések. 1. A legtöbb megoldó megfeledkezett arról, hogy a

v_{y}

sebeségkomponens a (14) egyenletben negatív szám (a labda már lefelé esik), de értelmezésünk szerint

tg β > 0

.
2. Egyetlen megoldó sem bizonyította be, hogy a (10) képletnek megfelelő szög valóban a legkisebb. Indoklás nélkül a megoldás természetesen nem teljes értékű. Azok a megoldók, akik jó eredményt hoztak ki, abból a helyes, de általuk nem indokolt állításból indultak ki, hogy a legkisebb szögben elhajított labda átmegy a kosár két szélső pontján. A megoldók többsége azonban abból a hamis feltevésből indult ki, hogy a leglaposabban induló pálya csúcspontja a kosár bal oldali szélső pontja lesz, és a jobb oldali pont alatt megy el a pontszerű labda. Eredményük természetesen hibás.