Feladat:	1155. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Frankó Ferenc ,  Karlócai Péter ,  Kiss Ildikó ,  Riba Mária ,  Végh Endre
Füzet:	1974/március, 137 - 138. oldal		PDF  |  MathML
Témakör(ök):	Csúszó súrlódás, Gördülés lejtőn, Pontrendszerek mozgásegyenletei, Feladat
Hivatkozás(ok):	Feladatok: 1973/október: 1155. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.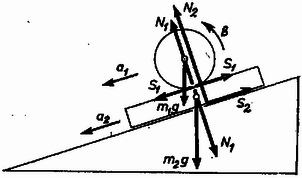     Az ábrán látható jelöléseket használva $(\Theta =\left(1/2\right)m{r}^2$ a henger tehetetlenségi nyomatéka) a mozgásegyenletek a következők: $\begin{array}{c}{\displaystyle m_1{a}_1=m_{1}g\text{sin}\alpha -S_1\mathrm{,}}\end{array}$ (1) $\begin{array}{c}{\displaystyle 0=m_{1}g\text{cos}\alpha -N_1\mathrm{,}}\end{array}$ (2) $\begin{array}{c}{\displaystyle \Theta \beta =S_1\cdot r\mathrm{,}}\end{array}$ (3) $\begin{array}{c}{\displaystyle m_2{a}_2=m_{2}g\text{sin}\alpha -S_2+S_1\mathrm{,}}\end{array}$ (4) $\begin{array}{c}{\displaystyle 0=m_{2}g\text{cos}\alpha -N_2+N_1\mathrm{.}}\end{array}$ (5) Tegyük fel, hogy mindkét érintkezésnél a felületek csúsznak egymáson. A súrlódási erők: $\begin{array}{c}{\displaystyle S_1=\mu N_1\mathrm{,}}\end{array}$ (6$a$) $\begin{array}{c}{\displaystyle S_2=\mu N_2\mathrm{.}}\end{array}$ (7$a$) Az egyenletrendszert megoldva, a gyorsulásokra $\begin{array}{c}{\displaystyle a_1=a_2=g\left(\text{sin}\alpha -\mu \text{cos}\alpha \right)}\end{array}$ adódik. Ez ellentmond feltételezésünknek, hiszen ekkor ‐ nyugalmi helyzetből való indulást feltételezve ‐ a henger és a deszka egymáshoz képest nem csúszhatnának. A felületek így az egyik, másik vagy mindkét érintkezési helyen összetapadnak. Tegyük fel, hogy csak a deszka csúszik meg a lejtőn, a henger tapad a deszkához. A (6$a$) egyenlet ekkor érvényét veszti (az $S_1\leqq \mu N_1$, egyenlőtlenség érvényes), helyette a tapadást kifejező kényszeregyenlet teljesül: $\begin{array}{c}{\displaystyle r\beta =a_1-a_2\mathrm{.}}\end{array}$ (6$b$) Az egyenletrendszerből (amely az (1), (2), (3), (4), (5), (6$b$), (7$a$) egyenletekből áll) $a_2$ értékét kifejezve negatív eredményt kapunk. Így ez a feltevés sem helytálló. Ha a deszka tapad a lejtőhöz, a (7$a$) egyenlet helyett az $\begin{array}{c}{\displaystyle a_2=0}\end{array}$ (7$b$) egyenlet érvényes. Feltételezve, hogy a henger viszont csúszva gurul lefelé, az (1), (2), (3), (4), (5), (6$a$), (7$b$) egyenletrendszert kell megoldanunk: $\begin{array}{c}{\displaystyle a_1=g\left(\text{sin}\alpha -\mu \text{cos}\alpha \right)\text{ és }\beta =\frac{2\mu g\text{cos}\alpha }{r}\mathrm{.}}\end{array}$ Feladatunk számadataival a csúszás feltétele, az $a_1\geqq r\cdot \beta$ egyenlőtlenség nem teljesül, így csak az a lehetőség marad, hogy a deszka nyugalomban marad, a henger pedig csúszásmentesen gördül a deszkán. A (6$b$) kényszeregyenletet figyelembe véve a megoldás: $\begin{array}{c}{\displaystyle a_1=\left(2/3\right)g\text{sin}\alpha \approx 1\mathrm{,}08{\text{m/s}}^2\mathrm{,}\beta =\left(2/3\right)\left(g/r\right)\text{sin}\alpha =13\mathrm{,}5{\text{l/s}}^2}\end{array}$  Riba Mária (Szeged, Ságvári E. Gyak. Gimn., III. o. t.),  Kiss Ildikó (Zalaegerszeg, Zrinyi M. Gimn., III. o. t.),  Frankó Ferenc (Szombathely, Nagy Lajos Gimn., IV. o. t.)  dolgozata alapján   Megjegyzés. A súrlódási határszög a feladatban adott $\mu =0\mathrm{,}14$ súrlódási együttható érték esetén $7^{\circ }58\text{'}$, kisebb, mint a lejtő hajlásszöge. A lejtőre helyezett deszka tehát lecsúszna róla. Amíg azonban a henger gördül a deszkán, a deszka nyugalomban marad. Ha a deszka nyugalomban marad és a henger tisztán gördül, akkor a következő összefüggéseknek kell teljesülniük: $\begin{array}{c}{\displaystyle S_1\leqq \mu m_{1}g\text{cos}\alpha \mathrm{,}{S}_2\leqq \mu \left(m_1+m_2\right)g\text{cos}\alpha \mathrm{,}{a}_2=\mathrm{0,}{a}_1=r\beta \mathrm{.}}\end{array}$ Ezek, valamint az (1), (2), (3), (4), (5) mozgásegyenletek felhasználásával $\text{tg }\alpha$-ra a következő megszorítást kapjuk: $\begin{array}{c}{\displaystyle \text{tg }\alpha \leqq \mu \frac{m_1+m_2}{\frac{m_1}{1+\frac{m_1{r}^2}{\theta }}+m_2}\mathrm{,}}\end{array}$ azaz a $7^{\circ }58\text{'}<\alpha <{10}^{\circ }15\text{'}$ szögtartományban lehetséges az, hogy a deszka nem csúszik meg mindaddig, amíg a henger rajta gördül. Könnyen belátható, hogy az egész szögtartományban valóban ez történik. Ha a lejtő hajlásszöge $7^{\circ }58\text{'}$-nél kisebb, a deszka önmagában sem csúszik meg, ha pedig ${10}^{\circ }15\text{'}$-nél nagyobb, a rajta gördülő henger ellenére is megcsúszik.    Karlócai Péter (Bp., Piarista Gimn., III. o. t.)  Végh Endre (Bonyhád, Petőfi S. Gimn., III. o. t.)