Kezdőlap


Feladat:	1148. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Benesóczki Dezső , Déri Klára , Sparing László , Szűcs István , Vladár Károly
Füzet:	1974/március, 131 - 134. oldal		PDF \| MathML
Témakör(ök):	Egyéb folyadék- és gázáramlás, Hidrosztatikai nyomás, Centrifugális erő, Gömbtükör, Feladat
Hivatkozás(ok):	Feladatok: 1973/szeptember: 1148. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Feltételezhetjük, hogy a szögsebesség változása olyan lassú, hogy a higany mozgását végig egyenletes forgómozgásnak tekinthetjük. Az 1102. feladat megoldásából (K. M. L. 47. kötet 1. szám 41. old.) tudjuk, hogy állandó $ω$ szögsebességgel forgatott edényben a folyadékfelszín forgás-paraboloid, keresztmetszetének egyenlete az 1. ábrának megfelelő koordináta-rendszerben

\begin{matrix} y = (ω^{2} / 2 g) x^{2} + C . \end{matrix}

(1)

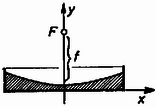1. ábra

Ezenkívül tudjuk még, hogy egy forgás-paraboloid alatti térfogat éppen a fele a testet magába foglaló henger térfogatának (2. ábra).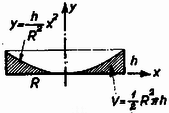

2. ábra

Szükségünk van még az (1) egyenlettel megadott parabola gyújtópontjának helyzetére is. Ha a gyújtópont és a parabola csúcspontjának távolságát

f

-fel jelöljük, akkor a parabola egyenletét

\begin{matrix} y = [1 / (4 f)] x^{2} + C \end{matrix}

alakban is írhatjuk. Összehasonlítva (1)-gyel, az adott szögsebességhez tartozó fókusztávolságra

f = g / (2 ω^{2})

adódik.
Feladatunkat legkönnyebben úgy oldhatjuk meg, ha végigkövetjük a folyadékfelszín időbeli változását. Induljunk ki egy álló hengerből (3. ábra).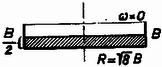

3. ábra

A higany félig tölti ki az edényt, felszíne sík.
Az edényt forgásba hozva a felszín forgás-paraboloid lesz, és egy bizonyos

ω

szögsebességnél a 4. ábrán látható alakzatot kapjuk.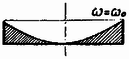

4. ábra

A térfogat állandóságából következik, hogy amikor a higany eléri az edény peremét, ugyanakkor az edény aljához is hozzáér a higanyfelszín. Határozzuk meg a gyújtópont helyzetét ebben az elrendezésben! A görbe egyenlete

\begin{matrix} y = (ω_{0}^{2} / 2 g) x^{2}, \end{matrix}

ezenkívül az

x = \sqrt[]{8} B

y = B

koordinátájú pont rajta fekszik a parabolán, tehát

\begin{matrix} B = (ω_{0}^{2} / 2 g) 8 B^{2}, \end{matrix}

ahonnan

\begin{matrix} ω_{0}^{2} = g / (4 B) . \end{matrix}

Ugyanakkor

f = g / (2 ω_{0}^{2}) = 2 B

, tehát a gyújtópont ‐ amely a szögsebesség növelésével egyre mélyebbre kerül ‐ már áthaladt a

4 B

magasan fekvő ponton, de a

B

magasságot még nem érte el.
Tovább kell tehát növelnünk a szögsebességet, de ekkor a higany egy része kifolyik az edényből és a fenéklap közepe is láthatóvá válik (5. ábra).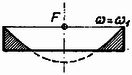

5. ábra

Amikor elérjük az

ω = ω_{1} = 5 s^{- 1}

szögsebességet, a gyújtópont

B

magasra kerül.
Ez az

\begin{matrix} y = (ω_{1}^{2} / 2 g) x^{2} + C_{1} \end{matrix}

egyenletű parabola adataival kifejezve annyit jelent, hogy

\begin{matrix} C_{1} + g / (2 ω_{1}^{2}) = B . \end{matrix}

(2)

Ezenkívül az

x = \sqrt[]{8} B

y = B

koordinátájú pont továbbra is a parabolán fekszik, tehát

\begin{matrix} B = (ω_{1}^{2} / 2 g) 8 B^{2} + C_{1} . \end{matrix}

(3)

A (2) és (3) egyenletekből

\begin{matrix} B = \frac{g}{\sqrt[]{8} ω_{1}^{2}} = 1, 39 dm, \end{matrix}

(4)

\begin{matrix} C_{1} = (1 - \sqrt[]{2}) B = - 0, 57 dm, \end{matrix}

\begin{matrix} f_{1} = \sqrt[]{2} B \end{matrix}

adódik. Eddig nem kellett sokat törődnünk az edényben levő higany térfogatával, mert az úgysem volt állandó, hanem a szögsebesség növelésével egyre csökkent. Ha viszont a szögsebességet csökkenteni kezdjük, a térfogat már állandó marad. Ezt az állandó térfogatot a 6. ábra alapján úgy határozhatjuk meg, hogy az

O B E

forgatásából származó forgás-paraboloid térfogatából levonjuk az

O A C

metszetű paraboloid és az

A B C D

metszetű hengeres gyűrű térfogatát.

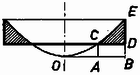6. ábra

Az eredmény:

\begin{matrix} V_{1} = 2 \sqrt[]{2} B^{3} π = 23, 7 {dm}^{3}, \end{matrix}

(5)

szemben az eredeti

\begin{matrix} V_{0} = 4 B^{3} π = 33, 6 {dm}^{3} \end{matrix}

(6)

térfogattal.
Ha most a szögsebességet csökkenteni kezdjük, a folyadék idővel felveszi a következő alakzatot (7. ábra).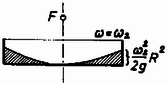

7. ábra

y = (ω_{2}^{2} / 2 g) x^{2}

görbe adatait a térfogat állandóságából határozhatjuk meg: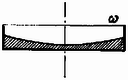

\begin{matrix} \frac{1}{2} {(\sqrt[]{8} B)}^{2} π \frac{ω_{2}^{2}}{2 g} {(\sqrt[]{8} B)}^{2} = V_{1}, \end{matrix}

ahonnan (5) felhasználásával

ω_{2}^{2} = \sqrt[]{2} g / (8 B)

és

f_{2} = 4 B / \sqrt[]{2} < 4 B

adódik. A gyújtópont még nem ért fel a

4 B

magasságig, tehát tovább kell csökkentenünk a szögsebességet. (Azért lényeges a kritikus

ω_{2}

‐ és korábban az

ω_{1}

‐ szögsebességhez tartozó gyújtóponthelyzetek meghatározása, hogy megtudjuk, vajon az 5. vagy pedig a 8. ábrának megfelelő alakzat térfogatát számoljuk.)

8. ábra

A görbe alakja tehát a 8. ábrán látható lesz, mikorra a fókusz

4 B

magasra kerül.

\begin{matrix} y = (ω^{2} / 2 g) x^{2} + C . \end{matrix}

A keresett

ω

szögsebességet a gyújtópont helyének és a térfogat nagyságának ismeretéből kaphatjuk meg:

\begin{matrix} 4 B = C + \frac{g}{2 ω^{2}}, \end{matrix}

(7)

\begin{matrix} R^{2} π (C + \frac{1}{2} \frac{ω^{2}}{2 g} R^{2}) = V . \end{matrix}

(8)

A gyújtópont kétszer is áthalad a

4 B

magasságú ponton: egyszer gyorsításkor, amikor még

V = V_{0}

, egyszer pedig lassításkor, amikor már

V = V_{1}

. A (7)‐(8) egyenletek ‐

C

-t kiküszöbölve ‐

ω^{2}

-re másodfokú egyenletet adnak, amelynek azonban csak a pozitív gyöke érdekel bennünket. Ez

\begin{matrix} V = V_{1} - nél ω = ω_{3} = 3, 01 s^{- 1}, \\ V = V_{0} - nál ω = ω_{4} = 3, 06 s^{- 1} . \end{matrix}

Megjegyzés. Az egész kísérlet lefutását a következő "folyamatdiagrammal'' szemléltethetjük (9. ábra).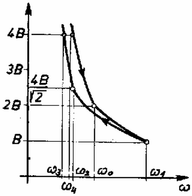

9. ábra

Ábrázoljuk a gyújtópont magasságát a szögsebesség függvényében! A nyíl a folyamat időbeli lefolyását jelzi. A görbe töréspontjai a 4. és 7. ábrán látható határeseteknél vannak. Ha a szögsebességet nem növeltük volna

ω_{0}

fölé, akkor a rendszer visszafelé ugyanazokon az állapotokon keresztül került volna nyugalmi helyzetébe. Jelen esetben azonban a rendszeren maradandó változást hoztunk létre (a higany egy része kifolyt), ezért visszafelé nem ugyanazt a görbét futjuk be a folyamatdiagramon. A jelenség hasonló a hiszterézissel rendelkező anyagok mágneses tér ‐ mágnesezettség diagramjához. Maradandó mágnesezettséget csak egy bizonyos értéknél erősebb mágnesező tér tud létrehozni.
Déri Klára (Kiskunhalas, Szilády Á. Gimn., IV. o. t.) és

Sparing László (Szombathely, Nagy Lajos Gimn., III. o. t.)
dolgozata alapján