Feladat:	1141. fizika feladat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Faragó Béla ,  Nagy Imre
Füzet:	1974/január, 44 - 46. oldal		PDF  |  MathML
Témakör(ök):	Tömegközéppont helye, Feladat
Hivatkozás(ok):	Feladatok: 1973/szeptember: 1141. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Szimmetrikus síkidomok súlypontja a szimmetria-középpontban, ill, a szimmetriatengelyen van. Ismeretes továbbá, hogy egy háromszöglemez súlypontja a háromszög geometriai súlypontjában van; és könnyen belátható, hogy ha egy háromszög csúcsaiban egyenlő nagyságú tömegpontokat helyezek el, akkor ezen rendszer súlypontja is a háromszög geometriai súlypontjában van. Legyen $AB=a$ a négyzet oldala. a) Az $ABECD$ ötszöget felbontom az $ABE$, $CDE$ és $DAE$ egybevágó háromszögekre (1. ábra). 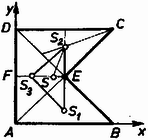    1. ábra   Ezek súlypontjai rendre $S_1$, $S_2$, $S_3$, a súlyvonalaknak az alaphoz közelebb eső harmadolópontjai. Mivel a háromszögek egyenlő területűek, az ötszög $S$ súlypontja megegyezik az $S_1{S}_2{S}_3$ háromszög súlypontjával: $\begin{array}{c}{\displaystyle E{S}_3=\left(2/3\right)EF;ES=\left(1/3\right)E{S}_3=a/9.}\end{array}$ A súlypont az $EF$ szimmetriatengelyen van $E$-től $a/9$ távolságra. b) Az $ABECDG$ hatszöget felbontom az $ABEG$ és $ECDG$ egybevágó paralelogrammákra (2. ábra). 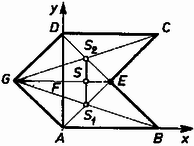    2. ábra Súlypontjuk, $S_1$, ill. $S_2$ az átlók felezőpontja. Mivel egyenlő területűek, a hatszög $S$ súlypontja megegyezik az $S_1{S}_2$ szakasz felezőpontjával: $\begin{array}{c}{\displaystyle ES=\left(1/2\right)EF=a/4.}\end{array}$ A súlypont az $EF$ szimmetriatengelyen van $E$-től $a/4$ távolságra. c) Az $AHKCD$ ötszöget felbontom az $AHBE$ és $BKCE$ négyzetekre és az $ACD$ derékszögű háromszögre (3. ábra). 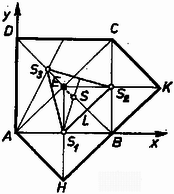    3. ábra Ezek súlypontjai rendre $S_1$, $S_2$, ill. $S_3$. Mivel a négyzetek és a háromszög területe egyenlő, az ötszög $S$ súlypontja egybeesik az $S_1{S}_2{S}_3$ háromszög súlypontjával. ${\displaystyle \begin{array}{c}\hfill {\displaystyle E{S}_3=\frac{1}{3}ED=\frac{a\sqrt[]{2}}{6}\mathrm{,}}\hfill \\ \hfill {\displaystyle S{S}_3=\frac{2}{3}L{S}_3=\frac{2}{3}\left(BE+E{S}_3-BL\right)=\frac{2}{3}\left(\frac{a\sqrt[]{2}}{2}+\frac{a\sqrt[]{2}}{6}-\frac{a\sqrt[]{2}}{4}\right)=\frac{5\sqrt[]{2}a}{18}\mathrm{,}}\hfill \end{array}}$ így $\begin{array}{c}{\displaystyle ES=S{S}_3-E{S}_3=\frac{5\sqrt[]{2}a}{18}-\frac{\sqrt[]{2}a}{6}=\frac{\sqrt[]{2}a}{9}\mathrm{.}}\end{array}$ A súlypont a $DB$ szimmetriatengelyen van $E$-től $\frac{a\sqrt[]{2}}{9}$ távolságra.   Nagy Imre (Szombathely, Nagy Lajos Gimn., II. o. t.)   II. megoldás. Ismeretes, hogy ($x_i\mathrm{,}{y}_i$) koordinátájú $m_i$ tömegpontokból ($i=\mathrm{1,}\text{...}\mathrm{,}n$) álló rendszer súlypontjának ($x_s\mathrm{,}{y}_s$) koordinátái (4. ábra) így számíthatók: $\begin{array}{c}{\displaystyle x_s=\frac{\Sigma m_i{x}_i}{\Sigma m_i}\mathrm{,}{y}_s=\frac{\Sigma m_i{y}_i}{\Sigma m_i}\mathrm{.}}\end{array}$     4. ábra Ezen képletek felhasználásával a síkidomok súlypontjának koordinátáit a következőképpen nyerhetjük. Helyezzük el az egyes síkidomokat az $x$, $y$ derékszögű koordinátarendszerben úgy, hogy $A$ az origóban; $B$ az $x$ tengely, $D$ pedig az $y$ tengely pozitív felén legyen. Bontsuk föl a szóbanforgó síkidomokat pl. az I. megoldásban leírt módon, és az egyes részeket helyettesítsük olyan tömegponttal, amely a rész súlypontjában van és nagysága számértékileg a síkidom területével egyenlő. Az így adódó pontrendszer súlypontjának koordinátáit számíthatjuk, a fenti képletek segítségével. A súlypontra az egyes esetekben a következőt kapjuk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle \text{<span style="font-style: italic;">a)</span>}S=\left(\frac{7}{18}a\mathrm{,}\frac{1}{2}a\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle \text{<span style="font-style: italic;">b)</span>}S=\left(\frac{1}{4}a\mathrm{,}\frac{1}{2}a\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle \text{<span style="font-style: italic;">c)</span>}S=\left(\frac{11}{18}a\mathrm{,}\frac{7}{18}a\right)\mathrm{,}}\hfill \end{array}}$ Faragó Béla (Csongrád, Batsányi J. Gimn., II. o. t.)