Kezdőlap


Feladat:	1100. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Lattmann Tibor
Füzet:	1973/május, 234 - 235. oldal		PDF \| MathML
Témakör(ök):	Egyenletesen változó mozgás (Tömegpont mozgásegyenelete), Körmozgás (Tömegpont mozgásegyenlete), Feladat, Hajítások
Hivatkozás(ok):	Feladatok: 1973/január: 1100. fizika feladat

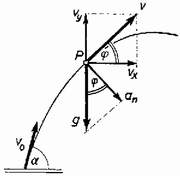
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az anyagi pont gyorsulása pályájának egy tetszés szerinti pontjában normális $(a_{n}$ ), és érintőleges $(a_{t})$ komponensekre bontható fel. A normális irányú gyorsulásösszetevő, valamint a pálya ezen pontjához tartozó görbületi sugár $(R)$ és a test (érintő irányú) $v$ sebessége között az

\begin{matrix} a_{n} = v^{2} / R \end{matrix}

(1)

összefüggés áll fenn.
Esetünkben a pálya parabola, bármely pontjában a kő gyorsulása a függőlegesen lefelé irányuló nehézség gyorsulás

(g)

φ

-vel jelöljük a parabolapálya

P

pontjában a függőleges és a normális közti (kisebbik) szöget, akkor ebben a pontban a normális irányú gyorsuláskomponens

\begin{matrix} a_{n} = g cos φ . \end{matrix}

(2)

φ

szög a

P

pontbeli sebességösszetevőkkel kifejezhető:

\begin{matrix} cos φ = \frac{v_{x}}{\sqrt[]{v_{x}^{2} + v_{y}^{2}}} . \end{matrix}

(3)

Az (1), (2) és (3) egyenletek egybevetéséből meghatározható a parabolapálya

P

pontjában a görbületi sugár:

\begin{matrix} R = \frac{{(v_{x}^{2} + v_{y}^{2})}^{3 / 2}}{y_{x}} . \end{matrix}

(4)

Az indulás után

t = 0, 5

s múlva elért pontban

\begin{matrix} v_{x} & = v_{0} cos α = v_{0} / 2 = 10 m/s, \\ v_{y} & = v_{0} sin α - g t = (\sqrt[]{3} / 2) v_{0} - g t = 12, 4 m/s, \end{matrix}

ezekből (4) alapján

R = 41, 3 m

. A parabolapálya legfelső pontjában

\begin{matrix} v_{x} & = 10 m/s \\ v_{y} & = 0, (4) alapján R = v_{x}^{2} / g = 10, 2 m \end{matrix}

Lattmann Tibor (Esztergom, Vegyipari Szakközépisk., III. o.t.) dolgozata alapján