Kezdőlap


Feladat:	1095. fizika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Lukács Gábor
Füzet:	1973/április, 189 - 190. oldal		PDF \| MathML
Témakör(ök):	Pontszerű töltés térerőssége, Szélsőérték differenciálszámítással, Coulomb-potenciál, Coulomb-energia, Feladat
Hivatkozás(ok):	Feladatok: 1972/december: 1095. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A probléma hengerszimmetriája miatt elegendő a két töltést tartalmazó tetszőleges síkban elvégezni a számításokat.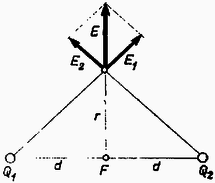
Legyenek a töltések $Q_{1}$ és $Q_{2}$ $(Q_{1} = Q_{2})$ , a létrehozott térerősségük $E_{1}$ és $E_{2}$ (a töltéseket összekötő szakasz felező merőlegesén $| E_{1} | = | E_{2} |$ ), s jelöljük $r$ -rel az $F$ felezőponttól a felező merőlegesen mért távolságot.

A felező merőlegesen az egyes töltések által létrehozott térerősség nagysága:

\begin{matrix} | E_{1} | = | E_{2} | = \frac{k Q}{r^{2} + d^{2}} . \end{matrix}

(1)

Az eredő térerősség nagysága a vektoriális őszszegezésből:

\begin{matrix} | E (r) | = | E_{1} | \frac{2 r}{\sqrt[]{r^{2} + d^{2}}}, & (2) \\ | E (r) | = \frac{2 k Q r}{{(r^{2} + d^{2})}^{3 / 2}}, & (3) \end{matrix}

iránya az ábrán látható.
Mivel

E (r)

r > 0

tartományban

r

-től függetlenül egy irányú, és

E (r)

a végtelenben nullához tart, ha a (3) függvénynek csupán egy szélsőértéke van, az csak maximum lehet.
Az első derivált

\begin{matrix} \frac{d | E |}{d r} = \frac{2 k Q}{{(r^{2} + d^{2})}^{5 / 2}} (d^{2} - 2 r^{2}) . \end{matrix}

(4)

r > 0

tartományban a derivált csak az

r = d \sqrt[]{2} / 2

helyen nulla, itt a derivált függvény előjelet is vált. Ez tehát a maximumhely.
A térbeli problémára visszatérve, a térerősség maximális értékét ‐ a két töltést összekötő szakasz felezőpontján átmenő merőleges síkon ‐ egy

F

középpontú,

r = d \sqrt[]{2} / 2

sugarú körön veszi fel. A térerősség maximális értéke itt:

\begin{matrix} E_{max} = \frac{4 \sqrt[]{3}}{9} \frac{Q}{d^{2}} . \end{matrix}

(5)

II. megoldás. A legtöbb elektromosságtani példánál előnyösebb potenciálokkal számolni, hiszen ezek a szuperpozíció elve szerint skalárisan adódnak össze, s így a bonyolultabb vektoriális összegzést elkerülhetjük. A potenciál gradiensének képzésével (egyenes mentén történő vizsgálatkor ez az első derivált) a térerősséget kapjuk.
Az I. megoldásban alkalmazott jelölésekkel:

\begin{matrix} U_{1} = U_{2} = - \frac{k Q}{\sqrt[]{r^{2} + d^{2}}} (6) U = U_{1} + U_{2} = - \frac{2 k Q}{\sqrt[]{r^{2} + d^{2}}}, (7) \end{matrix}

ahonnan

\begin{matrix} E (r) = \frac{d U}{d r} = \frac{2 k Q r}{{(r^{2} + d^{2})}^{3 / 2}}, \end{matrix}

(8)

A maximumhely megkeresése (matematikai probléma) innen már azonos az I. megoldásban mondottakkal.

Lukács Gábor (Budapest, Apáczai Cs. J. Gyak. Gimn., IV. o. t.)