Kezdőlap


Feladat:	1094. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Mihály László
Füzet:	1973/május, 228 - 231. oldal		PDF \| MathML
Témakör(ök):	Egyéb rögzített tengely körüli forgás, Párhuzamos erők eredője, Centrifugális erő, Tapadó súrlódás, Súrlódási határszög, Feladat
Hivatkozás(ok):	Feladatok: 1972/december: 1094. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Válasszunk forgó koordináta-rendszert, melyben a rúd nyugszik és rajzoljuk fel a rúdra ható erőket, figyelembe véve, hogy az 1014. feladat megoldása szerint a rúd egyes pontjaira ható centrifugális erők hatása két, a rúd végeitől $l / 3$ távolságban támadó $F_{c} = (m / 2) \cdot (R / 2) {(2 π n)}^{2}$ nagyságú erővel helyettesíthető (1. ábra).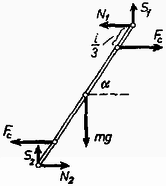

1. ábra

Az egyensúly feltétele az erőkre:

\begin{matrix} N_{1} - N_{2} = 0, & (1) \\ S_{1} + S_{2} - m g = 0, & (2) \end{matrix}

és a forgatónyomatékra:

\begin{matrix} (N_{1} + N_{2}) l \cdot sin α - 2 F_{c} \cdot (2 / 3) l \cdot sin α + (S_{1} - S_{2}) l \cdot cos α = 0, \end{matrix}

(3)

ahol

α

a rúd vízszintessel bezárt szöge.
Tudjuk, hogy a súrlódási erő abszolút értéke nem lehet nagyobb a nyomóerő és a súrlódási tényező szorzatánál:

\begin{matrix} - μ N_{1} \leq S_{1} \leq μ N_{1}, & (4) \\ - μ N_{2} \leq S_{2} \leq μ N_{2}, & (5) \end{matrix}

Kérdés, hogy milyen

μ

érték mellett teljesülnek az egyenletek és a feltételek.
Az (1) egyenlet felhasználásával és az

N_{1} = N_{2} = N

jelöléssel a (2) és (3) egyenletekből a következő képleteket kapjuk :

\begin{matrix} S_{1} = - N \cdot tg α + (m g / 2 + F_{c} \cdot (2 / 3) tg α), & (6) \\ S_{2} = N \cdot tg α + (m g / 2 - F_{c} \cdot (2 / 3) tg α) . & (7) \end{matrix}

Ábrázoljuk

S_{1}

-et és

S_{2}

-t mint

N

függvényét, és grafikonon tüntessük fel az

S_{1} = \pm μ N, S_{2} = \pm μ N

egyeneseket is !
Ha

\begin{matrix} (m g / 2) > F_{c} \cdot (2 / 3) tg α, \end{matrix}

(8)

akkor a 2. ábrán látható görbéket kapjuk.

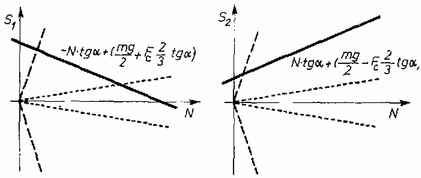2. ábra

A pontozott vonal felel meg annak az esetnek, amikor

μ < tg α

szaggatott vonalat

μ > tg α

esetén kapjuk. A (4), (5) feltétel teljesül, ha a (6), (7) függvények görbéje a feltételeket ábrázoló szögtartományon belül halad.
Látható, hogy az első esetben

N

lehetséges pozitív értékei között nincs olyan, amelynél az (5) feltétel teljesülne. (

S_{2}

görbéje sohasem kerül a szögtartományon belülre.) Ha viszont

μ > tg α

, akkor lehetséges egyensúlyi helyzet, mert elég nagy nyomóerőkre mindkét függvény képe a szögtartomány belsejében van.
Érdekesebb a helyzet, ha

\begin{matrix} m g / 2 < F_{c} (2 / 3) tg α, \end{matrix}

(9)

mert ekkor

S_{2}

N = 0

-nál negatív érték (3. ábra).

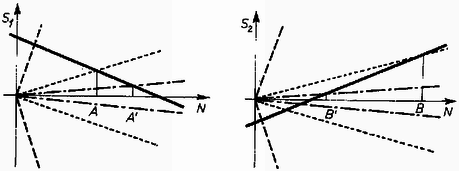3. ábra

Itt a következő lehetőségek vannak.
Ha

μ \geq tg α

, akkor biztos van olyan

N

, melynél a (4), (5) feltételek együtt teljesülnek (szaggatott vonal).
Ha

μ < tg α

, akkor bizonyos esetekben még mindig lehetséges egyensúlyi helyzet (pontozott vonal), de nincsen mindig egyensúly. Az

S_{1}

függvényből az

N > A

, az

S_{2}

függvényből az

N < B

feltételt kapjuk, és ha

B > A

, akkor van olyan

N

, amely mindkét kikötést teljesíti. Pl. nagyon kicsi

μ

értékeknél nem ez a helyzet

(B' < A'

, pont-vonallal ábrázolva), és nem lehetséges egyensúly. Határesetben

A = B

és figyelembe véve, hogy a metszéspontok koordinátája

\begin{matrix} A = \frac{m g / 2 + F_{c} \cdot (2 / 3) tg α}{μ + tg α}, & (10) \\ B = \frac{m g / 2 - F_{c} \cdot (2 / 3) tg α}{μ - tg α}, & (11) \end{matrix}

kapjuk, hogy

\begin{matrix} μ = (m g / F_{c}) \cdot (3 / 4) . \end{matrix}

(12)

Végeredményben a

\begin{matrix} μ \geq tg α, & (13) \\ μ \geq (m g / F_{c}) \cdot (3 / 4) & (14) \end{matrix}

feltételek egyikének teljesítésekor lehet a rúd nyugalomban. Mivel azonban a fenti számítás (9) alapján csak

tg α \geq (m g / F_{c}) \cdot (3 / 4)

esetén érvényes, nyilvánvaló, hogy (13) teljesülésekor (14) is igaz, és a két feltétel valójában egy. Figyelembe véve a centripetális erő értékét :

\begin{matrix} μ \geq (3 / 4) g / (π^{2} n^{2} R) . \end{matrix}

(15)

Vizsgáljuk meg az eredmény fizikai jelentését !

μ > tg α

azt jelenti, hogy a rúd a forgási sebességtől függetlenül beleszorul a hengerbe. Lehetséges, hogy a geometriai viszonyok ezt nem engedik meg, azonban ha a szögsebesség elég nagy, és teljesül a (9) feltétel:

\begin{matrix} F_{c} > (3 / 4) m g \cdot ctg α, azaz n > \sqrt[]{(3 / 4) (g / R) \cdot ctg α}, \end{matrix}

(16)

akkor még így is lehetséges stabil helyzet a (15)-ben megszabott súrlódási tényező esetén.
Megkérdezhetjük, hogy adott súrlódási tényező mellett mekkora erő nyomja a henger falát, és mekkorák a súrlódási erők. Az esetek többségében erre a kérdésre nem tudunk pontos választ adni, aminek az a magyarázata, hogy a vizsgált szerkezet sztatikailag határozatlan, a három egyenletből álló (1), (2), (3) egyenletrendszer négyismeretlenes. (Sztatikailag határozatlan szerkezetek csak akkor számíthatók, ha a rugalmasságtan egyenleteit is figyelembe vesszük.) Módszereinkkel az erők egyértelmű meghatározása csak akkor lehetséges, ha teljesül a (9) feltétel és a (12) egyenlőség, vagyis ha az

N

nyomóerő maximális és minimális értéke egybeesik. (10)-ből vagy (11)-ből kapjuk, hogy

N = (2 / 3) F_{c}

, és (1), (2), (3) mellé ezt negyedik egyenletnek véve a megoldás:

\begin{matrix} S_{1} = S_{2} = m g / 2, N = (2 / 3) F_{c} . \end{matrix}

Megjegyzés. A megoldók többsége a számítás kiinduló pontjának ‐ alaptalan szimmetria meggondolásokból ‐ az

S_{1} = S_{2} = m g / 2

egyenletet tekintette. Láthatjuk, hogy ez csak egy nagyon speciális

μ

érték mellett teljesül, és bizonyos mértékig szerencse, hogy így is a helyes eredményt kapjuk.
A fenti hiba miatt senki sem vette észre, hogy

μ > tg α

esetén a rúd az álló hengerben is benne marad.