Feladat: 1086. fizika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bari Ferenc ,  Fazekas Béla 
Füzet: 1973/április, 181 - 183. oldal  PDF  |  MathML 
Témakör(ök): Gördülés lejtőn, Súrlódás, Tapadó súrlódás, Csúszó súrlódás, Feladat
Hivatkozás(ok):Feladatok: 1972/november: 1086. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vizsgáljuk meg egy α hajlásszögű lejtőre helyezett m tömegű, r sugarú golyó mozgását, ha a súrlódási együttható μ. Jelöljük a golyó súlypontjának gyorsulását a-val, szöggyorsulását β-val és a tehetetlenségi nyomatékot Θ-val! A golyóra ható erőket vegyük fel az 1. ábrán látható módon!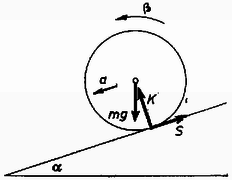

 

 

1. ábra
 

Két esetet kell megkülönböztetnünk. Ha a súrlódási együttható nem túl nagy, akkor a golyó gördül is és csúszik is a lejtőn. Ilyenkor a haladó- és forgómozgás egyenletei:
mgsinα-S=ma,(1)K-mgcosα=0,(2)Sr=Θβ.(3)
A súrlódási erő csúszó felületek között
S=μK.
Az egyenletrendszer megoldása Θ=(2/5)mr2 felhasználásával
a=g(sinα-μcosα),(4)β=5⋅μ⋅g⋅cosα2r(5)



Ez a megoldás csak akkor lehet helyes, ha a golyó forgásából származó kerületi gyorsulás nem nagyobb a haladó mozgás gyorsulásánál. (Ellenkező esetben a súrlódó felületek relatív elmozdulása ellentétes irányú lenne, és ilyenkor a súrlódási erő sem az ábrán felvett irányba mutatna.) A (4) és (5) megoldások felhasználásával és a gsinα-μgcosα≧(5/2)μgcosα összefüggésből μ-re a
μ≦(2/7)tg  α
megszorítást kapjuk.
Ha ez az egyenlőtlenség nem teljesül, akkor a golyó nem csúszik, hanem tiszta legördülést végez. Ilyenkor már nem érvényes a súrlódási erőre korábban felírt egyenlet, csupán az
S≦μ⋅K
egyenlőtlenség. Helyette viszont felhasználhatjuk, hogy a kerületi gyorsulás és a súlypont gyorsulása megegyezik, vagyis
rβ=a.(6)
Az (1), (2). és (3) összefüggések továbbra is érvényesek. Az egyenletrendszer megoldása
a=(5/7)gsinα,(7)
ami természetesen csak akkor jogos, ha μ≧(2/7)  tg  α.
Ábrázoljuk a haladó- és a forgómozgás gyorsulását a súrlódási együttható függvényében (2. ábra)!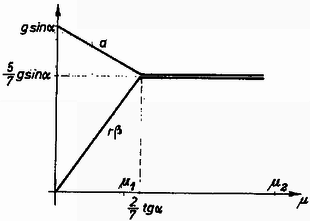
 

 

2. ábra
 

Látható, hogy nagyobb súrlódási együtthatóhoz kisebb vagy legfeljebb azonos súlyponti gyorsulás tartozik. A feladatban szereplő α=20∘-nál a kritikus súrlódási együttható
μ0=(2/7)  tg  α=0,104,
vagyis az egyik golyó (μ1=0,1) csúszva gördül, míg a másik (μ2=0,4) tiszta legördüléssel mozog. Az előbbinek határozottan nagyobb a gyorsulása, így előbb ér le a lejtő aljára.
Határozzuk meg az l hosszúságú lejtő alján a golyók haladási és forgás energiáit! Mindkét golyóra az
Ehaladási=(1/2)mv2=malésEforgási=(1/2)Θω2=(1/2)Θβ2t2
összefüggéseket használhatjuk, ahol t=2l/a a mozgás ideje. Az eltérés csupán annyi, hogy a megfelelő gyorsulásokat az egyik golyóra a (4) és (5), a másikra. pedig a (6) és (7) egyenletekből kapjuk.
a) A csúszva gördülő golyóra:
Ehaladási=mgl(sinα-μ1cosα)=4,87  J,Eforgási=52μ12cos2αsinα-μ1cosαmgl=1,75  J.
A teljes mozgási energia 6,62  J, a haladási és forgási energiák aránya 2,8.
b) A csúszásmentesen gördülő golyóra:
Ehaladási=(5/7)mglsinα=4,79  J,Eforgási=(2/7)mglsinα=1,92  J,
Az energiák aránya 5/2, a teljes mozgási energia pedig
Em=mglsinα=6,71  J.
Ez természetesen megegyezik a kezdeti potenciális energiával, hiszen csúszásmentes mozgásnál a teljes mechanikai energia nem változhat.
 

  Fazekas Béla (Budapest, Leövey K. Gimn., III. o. t.) dolgozata alapján
 

 

Megjegyzések. 1. A csúszó test mozgási energiáját is meg lehet határozni az energiamegmaradás tételének alkalmazásával, ha figyelembe vesszük a súrlódási erő WS munkavégzését:
Em=mglsinα-WS.
Vigyáznunk kell azonban WS kiszámításánál. WS=S⋅x, ahol x nem a lejtő hossza, hanem annál kevesebb, hiszen a golyó csúszás közben visszafelé elfordult. A relatív elmozdulás
x=t-rφ=a2t2-rβ2t2=l-lrβ/a.

 

  Bari Ferenc (Csongrád, Batsányi J. Gimn., IV. o. t.)
 

2. Sok versenyző arra a helytelen következtetésre jutott, hogy a második golyó el sem indul a lejtőn. A hibát ott követték el, hogy az S=μK egyenletet használták, ez pedig ‐ mint láttuk ‐ nem mindig érvényes.