Kezdőlap


Feladat:	1061. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balog János , Bari Ferenc , Bóc István , Drózdy Győző , Kövér András , Pataki Béla , Tegze Miklós
Füzet:	1973/január, 39 - 41. oldal		PDF \| MathML
Témakör(ök):	Rögzített tengely körüli forgás (Merev testek mozgásegyenletei), Egyéb merev test síkmozgások, Forgási energia, Feladat
Hivatkozás(ok):	Feladatok: 1972/május: 1061. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Vizsgáljuk először az a) esetet ! A rúd az $m g$ súlyerő és a falak $F_{1}$ és $F_{2}$ nyomóerőinek hatására az $A$ pont körül gyorsuló forgómozgást végez.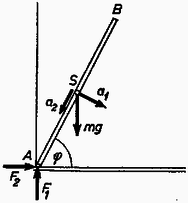

A súlypont gyorsulását felbonthatjuk érintőirányú

a_{1}

és rúdirányú

a_{2}

összetevőkre. Abban a pillanatban, amikor a rúd elválik a függőleges faltól,

F_{2}

-nek nullának kell lennie. Ekkor viszont vízszintes erő hiányában a súlypont gyorsulásának sem lehet vízszintes összetevője, vagyis

\begin{matrix} a_{1} sin φ - a_{2} cos φ = 0. \end{matrix}

(1)

a_{1}

nagyságát a forgómozgás alapegyenletéből számolhatjuk ki, felhasználva, hogy a rúd végpontjára

Θ_{A} = (1 / 3) m L^{2}

és

a_{1} = (L / 2) β

\begin{matrix} m \cdot g \cdot \frac{L}{2} cos φ = \frac{1}{3} \cdot m \cdot L^{2} \cdot \frac{2 a_{1}}{L}, \end{matrix}

(2)

ahonnan

a_{1} = \frac{3}{4} \cdot g \cdot cos φ

.
A rúdirányú gyorsulás az

ω

szögsebességgel kifejezve

\begin{matrix} a_{2} = \frac{L}{2} ω^{2} . \end{matrix}

Az energia-tétel alapján

\begin{matrix} m g \frac{L}{2} (1 - sin φ) = \frac{1}{2} \cdot \frac{1}{3} m L^{2} \cdot ω^{2}, ahonnan a_{2} = \frac{3}{2} g (1 - sin φ) \end{matrix}

(3)

adódik. Visszahelyettesítve (2)-t és (3)-at, az (1) összefüggésbe, az elválás szögére kapjuk

\begin{matrix} sin φ = 2 / 3, azaz φ \approx 42^{\circ} . \end{matrix}

A továbbiakban a súlypont sebességének vízszintes összetevője nem változik, megtartja a

\begin{matrix} v_{x} = \frac{L}{2} \cdot ω \cdot sin φ = \frac{1}{3} \sqrt[]{L g} \end{matrix}

(4)

értéket. A talajra érkezés pillanatában a súlypont

v_{s}

függőleges sebességét az energiamegmaradás tételéből számíthatjuk ki. Mivel az

A

pontnak nincs függőleges sebessége, ezért a rúdnak

ω' = \frac{v_{s}}{L / 2}

szögsebességgel kell rendelkeznie. A rúd teljes mozgási energiája a súlypont kinetikus energiája és az

\frac{1}{2} Θ_{s} \cdot ω'^{2}

forgási energia összegeként áll elő, ahol

Θ_{s} = \frac{1}{12} m L^{2}

a súlypontra vonatkoztatott tehetetlenségi nyomaték:

\begin{matrix} m g \frac{L}{2} = \frac{1}{2} m (v_{x}^{2} + v_{s}^{2}) + \frac{1}{2} \cdot \frac{1}{12} m L^{2} \cdot {(\frac{2 v_{s}}{L})}^{2}, \end{matrix}

ahonnan (4) felhasználásával

\begin{matrix} v_{s} = \sqrt[]{\frac{2 L g}{3}} \end{matrix}

adódik.
A földetérés pillanatában tehát az

A

pont

(1 / 3) \sqrt[]{L g}

vízszintes, a

B

pont ugyanekkor vízszintes és

2 v_{s} = \sqrt[]{\frac{8 L g}{3}}

függőleges sebességgel rendelkezik (a

B

pont teljes sebessége

5 \sqrt[]{L g} / 3

).
A b) esetben ugyanezeket a lépéseket végigkövetve valamennyi keresett mennyiségre ugyanazt az eredményt kapjuk, mint az a) esetben.

Bóc István (Bp., Apáczai Csere J. Gyak. Gimn., III. o. t.)

II. megoldás. Az energiatétel alkalmazásával tetszőleges

φ

szöghöz kiszámíthatjuk a súlypont sebességének vízszintes összetevőjét:

\begin{matrix} m g \frac{L}{2} (1 - sin φ) = \frac{1}{2} \cdot \frac{1}{3} m L^{2} ω^{2}, \\ v_{x} = \frac{L}{2} ω \cdot sin φ = \sqrt[]{\frac{3}{4} \cdot L \cdot g \cdot (1 - sin φ) sin^{2} φ} . & (5) \end{matrix}

Ez a függvény

φ

csökkenésével eleinte növekszik, majd egy maximumhely után csökkenni kezd. Másrészt a függőleges fal csak tolni tudja a rudat, ezért

v_{x}

nagysága nem csökkenhet. Az ellentmondás feloldása nyilván az, hogy (5) képlet csak a maximumhelyig érvényes, utána a rúd elválik a függőleges faltól és az összenergiához a haladó mozgás energiája is járulékot ad. A legnagyobb

v_{x}

-et az

f (φ) = (1 - sin φ) sin^{2} φ

függvény maximuma határozza meg, ezt viszont az

\begin{matrix} f' (φ) = 2 sin φ \cdot cos φ - 3 sin^{2} φ cos φ = 0 \end{matrix}

egyenlet megoldásai között kell keresnünk. A

cos φ = 0

és

sin φ = 0

egyenletek a sebességminimumokat adják meg, ezért a maximális sebesség elérését, vagyis a faltól való elválást a

\begin{matrix} sin φ = 2 / 3 \end{matrix}

összefüggés határozza meg.
A megoldás további menete azonos az I. megoldással. A b) esetben a súlypont végig ugyanolyan pályán mozog, mint az a) esetben, az energiatétel mindkét esetben azonos alakú, így a megoldások is megegyeznek.

Kövér András (Debrecen, KLTE Gyak Gimn., IV. o. t.)