Kezdőlap


Feladat:	986. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1972/január, 42 - 44. oldal		PDF \| MathML
Témakör(ök):	Merev test egyensúlya, Nyomóerő, kötélerő, Tapadó súrlódás, Feladat
Hivatkozás(ok):	Feladatok: 1971/május: 986. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Könnyen belátható, hogy a súlyzó csak akkor lehet egyensúlyban, ha a tengelyét és a gömb középpontját tartalmazó sík függőleges.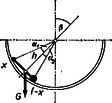
Jellemezzük a súlyzó helyzetét a súlypontját a gömb középpontjával összekötő egyenesnek a függőlegessel bezárt $β$ szögével! Az 1. ábrán látható $α_{1}$ , $α_{2}$ , $h$ értékek $m_{1}$ , $m_{2}$ , $m_{3}$ , $l$ és $r$ ismeretében a súlypont definíciójának felhasználásával meghatározhatók.

1. ábra

\begin{matrix} x = l \frac{m_{1} + m_{3} / 2}{m_{1} + m_{2} + m_{3}} \end{matrix}

akkor a súlyzó súlypontjának a félgömb középpontjától mért távolsága

\begin{matrix} h = \sqrt[]{r^{2} + x^{2} - l x}, továbbá cos α_{1} = \frac{2 r^{2} - l x}{2 r h}, cos α_{2} = \frac{2 r^{2} - l (l - x)}{2 r h} . \end{matrix}

A 2. ábrán felrajzoltuk a súlyzóra ható erőket.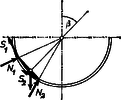

2. ábra

Az egyensúly feltétele: az erők összege és a forgatónyomatékok összege nulla.

\begin{matrix} N_{1} sin (β + α_{1}) - S_{1} cos (β + α_{1}) + N_{2} sin (β - α_{2}) - S_{2} cos (β - α_{2}) = 0, & (1) \\ N_{1} cos (β + α_{1}) + S_{1} sin (β + α_{1}) + N_{2} cos (β - α_{2}) + S_{2} sin (β - α_{2}) - G = 0, & (2) \\ S_{1} r + S_{2} r - G h sin β = 0, & (3) \end{matrix}

G = m_{1} g + m_{2} g + m_{3} g

.
Az

S_{1}

és

S_{2}

súrlódási erőkről csak annyit tudunk, hogy nagyságuk

\begin{matrix} | S_{1} | \leq μ N_{1}, (4) S_{2} | \leq μ N_{2} . (5) \end{matrix}

A (4) és (5) feltételt kielégítő, egyébként tetszőlegesen megválasztott súrlódási erőket az (1), (2), (3) egyenletrendszerbe helyettesítve megkapjuk a súlyzó egy lehetséges egyensúlyi helyzetét. Láthatjuk tehát, hogy az egyensúlyi helyzet nem pontosan határozott. Bizonyos azonban, hogy (4), (5)-nek megfelelően a súrlódási erők nagysága legfeljebb

| S_{1} | = μ N_{1}

| S_{2} | = μ N_{2}

lehet. Attól függően, hogy a súrlódási erők iránya a 2. ábrán berajzolttal egyezik vagy ellentétes, a fenti két egyenlőség alapján a következő egyenletpárokat kaphatjuk:

\begin{matrix} S_{1} = μ N_{1}, (4 a) & - S_{1} = μ N_{1}, (4 b) & - S_{1} = μ N_{1}, (4 c) & S_{1} = μ N_{1}, (4 d) \\ S_{2} = μ N_{2}, (5 a) & - S_{2} = μ N_{2}, (5 b) & S_{2} = μ N_{2}, (5 c) & - S_{2} = μ N_{2}, (5 d) \end{matrix}

(A 3. ábrán feltüntettük a súrlódási erők valódi irányát mind a négy esetben.)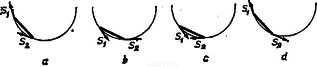

3. ábra

Az a), b), c), d) egyenletpárok bármelyikét is csatoljuk az (1), (2), (3) egyenletekhez, ötismeretlenes egyenletrendszert kapunk, melyet a matematikai nehézségek leküzdése után

β

-ra megoldhatunk.
Végeredményben az

α_{1} + α_{2} = α

jelöléssel:

\begin{matrix} ctg β_{a} = \frac{(h / μ r) (1 - μ^{2}) sin^{2} α + (cos α_{2} - cos α_{1}) sin α + (cos α_{2} + cos α_{1}) (1 - cos α) μ}{(sin α_{1} + sin α_{2}) sin α + (sin α_{2} - sin α_{1}) (1 - cos α) μ}, \\ ctg β_{b} = - \frac{(h / μ r) (1 - μ^{2}) sin^{2} α + (cos α_{1} - cos α_{2}) sin α + (cos α_{2} + cos α_{1}) (1 - cos α) μ}{(sin α_{1} + sin α_{2}) sin α + (sin α_{1} - sin α_{2}) (1 - cos α) μ}, \\ ctg β_{c} = \frac{(l / μ r) \frac{μ^{2} (1 + cos^{2} α) + sin^{2} α - 2 μ cos α sin α}{μ (cos α - 1) - sin α} - cos α_{1} + cos α_{2}}{sin α_{1} + sin α_{2}}, \\ ctg β_{d} = \frac{(l / μ r) \frac{μ^{2} (1 + cos^{2} α) + sin^{2} α + 2 μ cos α sin α}{μ (cos α - 1) + sin α} - cos α_{1} + cos α_{2}}{sin α_{1} + sin α_{2}}, \end{matrix}

A súlyzó két szélső helyzetét nem túl nagy

μ

esetén

β_{a}

és

β_{b}

határozza meg.

β_{b}

negatív előjele kifejezi azt, hogy ekkor a súlyzó a 2. ábrán láthatóval ellentétes oldalon van. Ellenőrizhetjük, hogy a kapott eredmény egyes speciális esetekben (

α_{1} = α_{2} = α = 0

α_{1} = α_{2}

μ = 0

) is helyes értéket ad.

β_{d}

-ből ‐ mint az a 3d ábra alapján várható volt ‐ semmi érdekes következtetést sem tudunk levonni. Érdemes megfigyelni, hogy amennyiben

μ (cos α - 1) = sin α

, akkor a c) esetben

β_{c}

értéke független a súlypont helyzetétől. Ez annak felel meg, hogy a súlyzó beszorul a gömbbe, aminek feltétele egyszerűbb alakban:

\begin{matrix} ctg \frac{α}{2} = μ . \end{matrix}

Ha tehát a súrlódási tényező eílég nagy, akkor a súlyzó bárhol egyensúlyban lehet. A fenti eredmény hasonló az ék vizsgálatánál kapott feltételhez.

Megjegyzés. Sok megoldó abból a feltevésből indult ki, hogy

S = μ m g cos α

, ami csak egyes speciális esetekben igaz. Általában célszerű a fentihez hasonló gondolatmenettel egyenletrendszert felállítani.
Voltak, akik csak az egyenleteket írták fel, és nem is próbálkoztak azok megoldásával. Így a feladat megoldásának nagyon tanulságos részét mulasztották el.
Senki sem vette észre, hogy a súlyzó beszorulhat a gömbbe.