Kezdőlap


Feladat:	975. fizika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Magyar László
Füzet:	1971/december, 236 - 237. oldal		PDF \| MathML
Témakör(ök):	Pontszerű töltés térerőssége, Megosztás, Felületi töltéssűrűség, Feladat
Hivatkozás(ok):	Feladatok: 1971/március: 975. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha a zérus potenciálú felületet földelt fémlemezzel helyettesítjük, az erőtérben semmi sem változik, hiszen a földelt fémlemez potenciálja zérus. Ezért a térerősség ugyanakkora marad, mint a fémlemez odahelyezése előtt volt.
Vegyük fel a koordinátarendszer origóját a $Q_{1}$ töltés helyén. $Q_{2}$ koordinátái legyenek: $(0, d,0)$ . Határozzuk meg azon $P$ $(x, y, z)$ pontok mértani helyét, melyekre a potenciál értéke zérus! A

\begin{matrix} \frac{Q_{1}}{{(x^{2} + y^{2} + x^{2})}^{1 / 2}} + \frac{Q_{2}}{{[x^{2} + {(y - d)}^{2} + z^{2}]}^{1 / 2}} = 0 \end{matrix}

(1)

egyenletet nyerjük, melyből

x^{2} + y^{2} + z^{2} = r^{2}

és

k = | \frac{Q_{2}}{Q_{1}} |

jelöléssel a zérus potenciálú felület egyenlete:

\begin{matrix} (1 - k^{2}) r^{2} = d (2 y - d) . \end{matrix}

(2)

Q_{1} = - Q_{2}

, tehát

k = 1

. A zérus potenciálú felület az

y = d / 2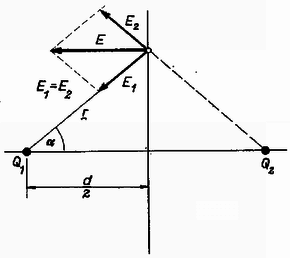

sík.

1. ábra

Az 1. ábra alapján a térerősség:

\begin{matrix} E = 2 E_{1} cos α = 2 E_{1} \cdot \frac{d}{2 r} = E_{1} \cdot \frac{d}{r} . & (3) \\ Mivel E_{1} = \frac{1}{4 π ε_{0}} \frac{Q_{1}}{r^{2}}, & (4) \\ E = \frac{1}{4 π ε_{0}} \frac{Q_{1} d}{r^{3}} . & (5) \end{matrix}

A felületi töltéssűrűség definíció szerint:

\begin{matrix} σ = ε_{0} E = \frac{1}{4 π} \frac{Q_{1} d}{r^{3}} . \end{matrix}

(6)

A feladat számadataival (ha

r

-et méterben mérjük):

\begin{matrix} E = \frac{90}{r^{3}} [\frac{V}{m}], és σ \approx \frac{8 \cdot 10^{- 10}}{r^{3}} [\frac{C}{m^{2}}] \end{matrix}

b) A zérus potenciálú felület egyenlete

Q_{1} \neq - Q_{2}

esetben:

\begin{matrix} x^{2} + {(y \frac{d}{1 - k^{2}})}^{2} + z^{2} = {(\frac{k d}{k^{2} - 1})}^{2} . \end{matrix}

Ez a felület tehát egy gömb, melynek középpontja az

O (0, \frac{d}{1 - k^{2}},0)

pontban van, sugara:

r_{0} = \frac{k d}{k^{2} - 1}

(a feladat számadataival: O (0, - \frac{1}{15},0) és r_{0} = \frac{4}{15})

.
Határozzuk meg a térerősség nagyságát egy olyan körön, amelyet egy ‐ a két töltésen átmenő ‐ sík metsz ki a gömbből! Vegyük figyelembe, hogy az erő vonalak az ekvipotenciális felületre merőlegesek, és helyezzük a koordinátarendszer origóját a gömb középpontjába!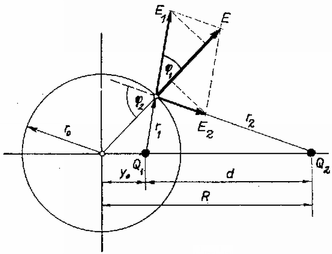

2. ábra

A 2. ábra alapján

\begin{matrix} E = E_{1} cos φ + E_{2} cos φ_{2} . \end{matrix}

(8)

Cosinus ‐ tétellel

cos φ_{1}

és

cos φ_{2}

kifejezhető:

\begin{matrix} cos φ_{1} & = \frac{r_{0}^{2} + r_{1}^{2} - y_{0}^{2}}{2 r_{0} r_{1}}, & (9) \\ cos φ_{2} & = \frac{R_{0}^{2} + r_{0}^{2} - y_{2}^{2}}{2 r_{0} r_{2}}, & (10) \end{matrix}

Felhasználva a (8) ‐ (10), továbbá a

k r_{1} = r_{2}

k Q_{1} = Q_{2}

és

k y_{0} = r_{0}

összefüggéseket:

\begin{matrix} E = \frac{1}{4 π ε_{0}} \frac{Q_{2}}{r_{2}^{3}} \frac{1}{2 r_{0}} {k^{2} (r_{0}^{2} + r_{1}^{2} - y_{0}^{2}) + R^{2} - r_{0}^{2} - r_{2}^{2}} = \\ = \frac{1}{4 π ε_{0}} \frac{Q_{2}}{r_{2}^{3}} \frac{1}{2 r_{0}} {(k^{2} - 1) r_{0}^{2} + R^{2} - k^{2} y_{0}^{2}} . & (11) \end{matrix}

Vegyük figyelembe még, hogy

k r_{0} = R

'es

R = d + y_{0}

. Ezzel

\begin{matrix} E = \frac{Q_{2}}{4 π ε_{0}} [\frac{{(d + y_{0})}^{2} - r_{0}^{2}}{r_{0}}] \frac{1}{r_{2}^{3}} \end{matrix}

(12)

adódik. A felületi töltéssűrűség

\begin{matrix} σ = ε_{0} E = \frac{Q_{2}}{4 π} [\frac{{(d + y_{0})}^{2} - r_{0}^{2}}{r_{0}}] \frac{1}{r_{2}^{3}} . \end{matrix}

(13)

A feladat számadataival

\begin{matrix} E = \frac{1440}{r_{2}^{3}} [\frac{V}{m}], és σ = 1, 27 \cdot 10^{- 8} \cdot \frac{1}{r_{2}^{3}} [\frac{C}{m^{2}}] . \end{matrix}

Magyar László (Kecskemét, Katona J. Gimn., IV. o. t.)