Kezdőlap


Feladat:	944. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bognár Béla , Dózsa Márton , Gál Péter , Nagy István , Zimmermann Miklós
Füzet:	1971/május, 231 - 233. oldal		PDF \| MathML
Témakör(ök):	Egyéb ellenállás-kapcsolások, Ellenállásmérés, Feladat
Hivatkozás(ok):	Feladatok: 1970/november: 944. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Veszünk $n$ pontot (1. ábra).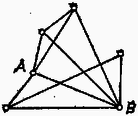

1. ábra

Válasszunk ki tetszőleges kettőt (

A

és

B

R

ellenállású vezetőkkel kössük össze a megmaradt pontokat

A

-val, ill.

B

-vel, és

A

-t

B

-vel. Az

A

B

pontokra feszültséget kötve, a megmaradt pontok ekvipotenciális pontok. Ezért az elrendezést teljes sokszöggé kiegészítve, az eredő ellenállás nem változik.
Az egyszerűsített rendszerben

n - 2

2 R

és egy

R

nagyságú ellenállás van párhuzamosan kötve, így

\begin{matrix} \frac{1}{R_{e}} = \frac{1}{R} + \frac{n - 2}{2 R}, R_{e} = \frac{2 R}{n} . \end{matrix}

Nagy István (Bp., Móricz Zs. Gimn., IV. o. t.)

II. megoldás. Válasszuk ki a teljes sokszög két tetszőleges pontját (

A

és

B

). Minden egyes megmaradt pont

A

-hoz,

B

-hez és a többi megmaradt ponthoz ugyanolyan módon csatlakozik, egyik sincs kitüntetve, így az

A

B

pontokra feszültséget kötve, a maradék pontok ekvipotenciálás pontok lesznek. Tehát a maradékpontokat összekötő ellenállások elhagyhatók. Tovább, mint az I. megoldásban.

Bognár Béla (Sopron, Széchenyi I. Gimn., IV. o. t.)

III. megoldás. Válasszuk ki a teljes sokszög két tetszőleges pontját, majd ezekkel kezdve, számozzuk meg a pontokat:

A_{1}, A_{2}, ..., A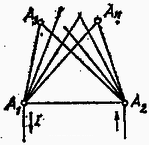_{n}

(2. ábra).

2. ábra

Kössünk

U

feszültséget az

A_{1}

és

A_{2}

pont közé. Ekkor az

A_{i}

pont feszültsége

U_{i}

, és az

A_{i}

, ill.

A_{j}

pontok között folyó áram

\begin{matrix} I_{i j} = \frac{U_{i} - U_{j}}{R} . \end{matrix}

Fölírjuk a csomóponti törvényt az

A_{1}

és

A_{2}

pontokra:

\begin{matrix} I = \sum_{i = 1}^{n} I_{1 i} = \sum_{i = 1}^{n} \frac{U_{1} - U_{i}}{R} = \frac{n U_{1}}{R} - \frac{1}{R} \sum_{i = 1}^{n} U_{i}, \\ I = \sum_{i = 1}^{n} I_{i 2} = \sum_{i = 1}^{n} \frac{U_{i} - U_{2}}{R} = \frac{1}{R} \sum_{i = 1}^{n} U_{i} - \frac{n U_{2}}{R} . \end{matrix}

(Felhasználtuk, hogy I_{11} = \frac{U_{1} - U_{1}}{R} = 0 = I_{22} .)

A két fenti egyenletet összeadva:

\begin{matrix} 2 I = \frac{n}{R} (U_{1} - U_{2}) = \frac{n U}{R} . \end{matrix}

Az eredő ellenállás:

\begin{matrix} R_{e} = \frac{U}{I} = \frac{2 R}{n} . \end{matrix}

Gál Péter (Bp., Fazekas M. Gimn., III. o. t.)

Megjegyzések. 1. Sokan egyáltalán nem, vagy nem kielégítően bizonyították, hogy a "maradék pontok'' ekvipotenciális pontok, pedig a megoldásnak ez fontos lépése.
2. A feladat eredménye szerint egy

n

sarokpontból álló teljes sokszög eredő ellenállása egyenlő komponens-ellenállások

(R)

esetén:

\begin{matrix} R_{e} = \frac{2 R}{n} . \end{matrix}

Ez az eredmény módot ad rá, hogy megállapíthassuk, miként lehet egy

n

ágú csillagot

n

szögű teljes sokszöggé alakítani, ha az összes ellenállások egyenlők az egyes alakzatokban.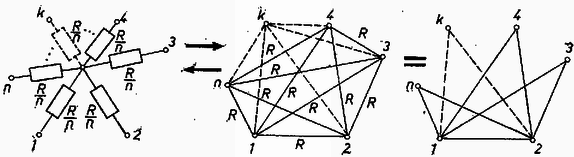

3. ábra

Nyilván, mint a 3. ábrán látható

R_{12} = \frac{2 R}{n} = R_{e}

, vagyis a csillag bármelyik két pontja közötti ellenállás egyenlő a teljes sokszög eredő ellenállásával. A háromszög-csillag átalakításnál ez közismert (4. ábra).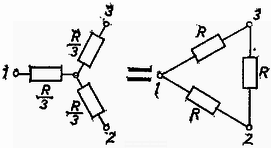

4. ábra

Dózsa Márton