Kezdőlap


Feladat:	940. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Éber Nándor
Füzet:	1971/április, 189 - 190. oldal		PDF \| MathML
Témakör(ök):	Rögzített tengely körüli forgás (Merev testek mozgásegyenletei), Közelítő számítások, numerikus módszerek, Feladat
Hivatkozás(ok):	Feladatok: 1970/november: 940. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Számítsuk ki, hogy ha a rúd a vízszintessel $α$ szöget zár be, mekkora a rúd pillanatnyi szöggyorsulása.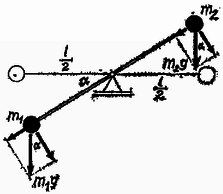

A forgatónyomatékok összege

\begin{matrix} M = m_{1} g (l / 2) cos α - m_{2} g (l / 2) cos α = (m_{1} - m_{2}) g (l / 2) cos α . \end{matrix}

A rendszer tehetetlenségi nyomatéka

\begin{matrix} Θ = m_{1} {(\frac{l}{2})}^{2} + m_{2} {(\frac{l}{2})}^{2}, így \\ β = \frac{M}{Θ} = \frac{2 g (m_{1} - m_{2}) cos α}{(m_{1} + m_{2}) l} . \end{matrix}

A szöggyorsulás tehát a mozgás során változik.
A mozgás ideje azonban rövid, így ‐ mint látni fogjuk ‐, nem követünk el nagy hibát, ha

β

-t állandónak vesszük. Legyen először

α = 0

, ekkor

\begin{matrix} β_{1} = \frac{2 g}{t} \cdot \frac{m_{1} - m_{2}}{m_{1} + m_{2}} = 5 s^{- 2} (g = 10 {m s}^{- 2}) . \end{matrix}

Az ekkorának tekintett állandó szöggyorsulással az elfordulás

\begin{matrix} α_{1} = \frac{β_{1}}{2} t^{2} = 2, 5 s^{- 2} \cdot 0, 1^{2} s^{2} = 0, 025 = 1^{\circ} 26' . \end{matrix}

Ez az érték nagyobb a tényleges

α

szögelfordulásnál, hiszen

β_{1}

a szöggyorsulás maximuma. Mivel a szögelfordulás mindig kisebb

α_{1}

-nél, ezért

β

nagyobb az

α_{1}

kitéréshez tartozó értéknél. Ha tehát

β

-t az egész mozgás során az

α_{1}

-hez tartozó értéknek vesszük

(β_{2})

, akkor az elfordulásra alsó becslést kapunk.
Végezzük el ennek megfelelően a számolást:

\begin{matrix} β_{2} & = \frac{2 g}{l} \frac{m_{1} - m_{2}}{m_{1} + m_{2}} cos α_{1} = β_{1} cos α_{1}, \\ α_{2} & = \frac{β_{2}}{2} t^{2} = α_{1} cos α_{1} = α_{1} \cdot 0, 9997. \end{matrix}

Így

\begin{matrix} α_{2} = α_{1} \cdot 0, 9997 < α < α_{1} . \end{matrix}

Tehát

0, 03 %

hibával

α = α_{1}

, ezért a tömegek elmozdulása

\begin{matrix} s = \frac{l}{2} α_{1} = 1, 25 cm . \end{matrix}

Éber Nándor (Budapest, Móricz Zs. Gimn., III. o. t.)