Kezdőlap


Feladat:	903. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Harmat Péter , Klebniczki József , Mihály György
Füzet:	1971/január, 38 - 40. oldal		PDF \| MathML
Témakör(ök):	Felületi feszültségből származó erő, Felületi feszültségből származó energia, Erők forgatónyomatéka, Összetartó erők eredője, Szélsőérték differenciálszámítással, Feladat
Hivatkozás(ok):	Feladatok: 1970/március: 903. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A keret alakját egyértelműen jellemezhetjük a léceknek a vízszintestől mért $α$ hajlásszögével. A keretre az 1. ábrán látható erők hatnak.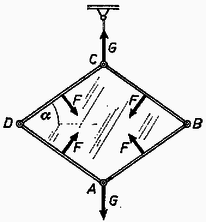

1. ábra

Mivel a folyadékhártyának két szabad felülete van, ezért

F = 2 l σ

. Ha az egész keretre írjuk fel a külső erők és forgatónyomatékok egyensúlyát, azonosságot kapunk. Az

F

G

és

α

közti összefüggést csak akkor tudjuk meghatározni, ha kihasználjuk, hogy a keret egyes darabjai külön-külön is egyensúlyban vannak. Írjuk fel pl. az

A B

szakasz egyensúlyának feltételét! A rúd végpontjában a csuklók a 2. ábrán látható erőkkel nyomják a rudat.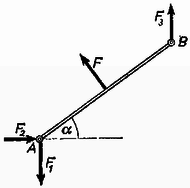

2. ábra

Szimmetriaokokból a

B

pontban csak függőleges erő hat. Kapjuk tehát, hogy

\begin{matrix} F cos α + F_{3} - F_{1} = 0, & (1) \\ F_{2} - F sin α = 0. & (2) \end{matrix}

A forgatónyomatékot írjuk fel a

B

pontra!

\begin{matrix} F (l / 2) - F_{1} l cos α - F_{2} l sin α = 0. \end{matrix}

(3)

Ebben a három egyenletben három ismeretlen erő és az

α

szög szerepel. A hiányzó egyenletet az

A

pontban levő csuklóra ható erők egyensúlya szolgáltatja.

3. ábra

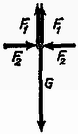A szimmetrikus elrendezés miatt az

A B

és

A D

rudak reakcióerejének függőleges komponense azonos nagyságú (3. ábra):

\begin{matrix} 2 F_{1} - G = 0. \end{matrix}

(4)

Az (1)‐(4) egyenletrendszerből

cos α

-ra a következő egyenletet kapjuk:

\begin{matrix} 2 F cos^{2} α - G cos α - F = 0, \end{matrix}

(5)

ahonnan

\begin{matrix} cos α = \frac{G}{4 F} \pm \sqrt[]{{(\frac{G}{4 F})}^{2} + \frac{1}{2}} . \end{matrix}

Mivel

0 < α < 90^{\circ}

, azért a négyzetgyököt pozitív előjellel kell vennünk. A

cos α < 1

feltétel akkor teljesül, ha

G < F

. Amennyiben ez nem áll fenn, úgy nem jöhet létre egyensúly a fenti erők hatására. A keret egészen

α = 90^{\circ}

-ig deformálódik, ekkor a

B

és

D

csuklók érintkezésénél fellépő vízszintes erők állítják vissza az erőegyensúlyt. Hasonlóan

α = 0^{\circ}

-nál is létrejöhet az

A

és

C

csuklók közt fellépő erők hatására. Ennek feltételét, valamint az egyes egyensúlyi helyzetek stabilitását kényelmesebb az energiaviszonyok tanulmányozásával meghatározni.

Harmat Péter (Mosonmagyaróvár, Kossuth L. Gimn., II. o.t.)

II. megoldás. Vizsgáljuk meg a rendszer energiáját az

α

szög függvényében. A keret által határolt terület

A = l^{0} sin α

. Mivel a felületi feszültség egyik definíciója szerint a felületegységre eső energiát jelenti, ezért (figyelembe véve, a folyadékhártya mindkét felszínét) a felületi energia:

\begin{matrix} E_{1} = 2 A σ . \end{matrix}

G

súlyú test helyzeti energiája a

C

ponthoz viszonyítva

\begin{matrix} E_{2} = - 2 l (sin α) G . \end{matrix}

A teljes energia

\begin{matrix} E = 2 l^{2} σ sin 2 α - 2 l (sin α) G . \end{matrix}

Ha ábrázoljuk

E

-t a függvényében, akkor

G ⋚ 2 l σ

eseteknek megfelelően 3 különböző jellegű görbét kapunk (4. ábra).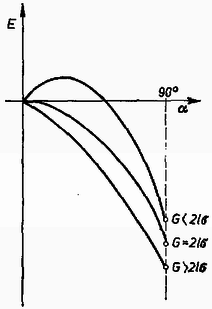

4. ábra

Stabil egyensúly ott alakul ki, ahol az energiának minimuma van. Ez mindig teljesül az

α = 90^{\circ}

-os szögnél, valamint

G < 2 l σ

esetben

α = 0^{\circ}

-nál is. Ahol az energiának maximuma van, ott a rendszer instabil egyensúlyi helyzete található. A

G > 2 l σ

esetben ez sohasem teljesül, a

G \leq 2 l σ

esetben pedig valamilyen

α

szögnél. Ez a szög a differenciálszámítás segítségével határozható meg, mivel

α_{0}

értéknél

\begin{matrix} E' = 4 l^{2} σ cos 2 α_{0} - 2 l G cos α_{0} = 0. \end{matrix}

Ebből egyszerű átalakításokkal megkaphatjuk az (5) egyenletet.

Határesetben, ha

G = 2 l σ

, akkor

α_{0} = 0^{\circ}

Klebniezki József (Szeged, Ságvári E. Gimn., III. o. t.)