Kezdőlap


Feladat:	899. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Berkes Enikő , Blahó Ágnes , Bodnár István , Boros Endre , Gács Lajos , Gál Péter , Hernádi Zsuzsanna , Komornik Vilmos , Kramer András , Magyar András , Nagy Péter , Pataki Béla , Reviczky János , Sebestyén Péter , Simon László , Szabó László , Torma Tibor
Füzet:	1971/január, 34 - 35. oldal		PDF \| MathML
Témakör(ök):	Csigasor, Pontrendszerek mozgásegyenletei, Feladat
Hivatkozás(ok):	Feladatok: 1970/március: 899. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A csigák és a kötelek súlytalanok, súrlódás nincs, vagyis az egyes kötéldarabokat végig ugyanaz az erő feszíti, függetlenül attól, hogy a kötéldarab egyenes, vagy csigákat kerül-e meg. Feladatunkban tíz kötéldarab szerepel.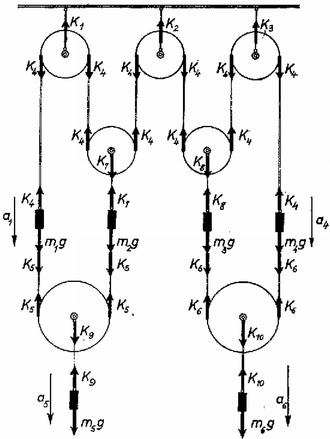

1. ábra

A hat tömegre, valamint a hét csigára írjuk fel a mozgásegyenleteket (Newton II. törvénye). Az 1. ábrán láthatók az egyes testekre ható erők. Jelöljük az

m_{1}

tömegű test gyorsulását

a_{1}

-gyel, az

m_{2}

-ét

a_{2}

-vel,

...

, az

m_{6}

-ét

a_{6}

-tal, és válasszuk a pozitív irányt minden esetben lefelé.

A mozgásegyenletek a hat tömegpontra:

\begin{matrix} m_{1} a_{1} = m_{1} g + K_{5} - K_{4}, & (1) \\ m_{2} a_{2} = m_{2} g + K_{5} - K_{7}, & (2) \\ m_{3} a_{3} = m_{3} g + K_{6} - K_{8}, & (3) \\ m_{4} a_{4} = m_{4} g + K_{6} - K_{4}, & (4) \\ m_{5} a_{5} = m_{5} g - K_{9}, & (5) \\ m_{6} a_{6} = m_{6} g - K_{10} . & (6) \end{matrix}

A csigák tömege nulla, vagyis mozgásegyenletük bal oldala a gyorsulásoktól függetlenül nulla:

\begin{matrix} 0 = K_{1} - 2 K_{4}, (7) & 0 = K_{2} - 2 K_{4}, (8) \\ 0 = K_{3} - 2 K_{4}, (9) & 0 = 2 K_{4} - K_{7}, (10) \\ 0 = 2 K_{4} - K_{8}, (11) & 0 = 2 K_{5} - K_{9}, (12) \\ 0 = 2 K_{6} - K_{10} . (13) \end{matrix}

16 ismeretlenünkhöz még csak 13 egyenlet van. A hiányzó egyenletek azt fejezik ki, hogy a kötelek nyújthatatlanok: a gyorsulások nem függetlenek egymástól (kényszer feltétel). A 2. ábrán a bal alsó csigát és környezetét rajzoltuk le az indulás pillanatában és

t

idővel később.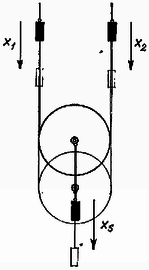

2. ábra

Jelöljük az

m_{1}

m_{2}

és

m_{3}

test elmozdulásait

x_{1}

x_{2}

és

x_{5}

-tel. A fonál nyújthatatlan, vagyis

\begin{matrix} x_{1} + x_{2} = 2 x_{5} . \end{matrix}

\begin{matrix} x_{1} = (1 / 2) a_{1} t^{2}, x_{2} = (1 / 2) a_{2} t^{2}, x_{5} = (1 / 2) a_{5} t^{2} \end{matrix}

egyenlőségeket behelyettesítve kapjuk, hogy

\begin{matrix} a_{1} + a_{2} = 2 a_{5} . \end{matrix}

(14)

Hasonlóan

\begin{matrix} a_{3} + a_{4} = 2 a_{6} . \end{matrix}

(15)

Az előző mintára mozdítsuk az

m_{1}

m_{2}

és

m_{3}

tömegeket lefelé

x_{1}

x_{2}

és

x_{3}

távolsággal, ekkor az

m_{4}

tömeg

x_{4}

elmozdulása már adódik:

\begin{matrix} x_{4} = - (x_{1} + 2 x_{2} + 2 x_{3}), \end{matrix}

mert közben a

K_{4}

feszültségű fonál hossza állandó maradt.

Ezekre az elmozdulásokra

\begin{matrix} x_{1} = (1 / 2) a_{1} t^{2}, & x_{2} = (1 / 2) a_{2} t^{2}, \\ x_{3} = (1 / 2) a_{3} t^{2}, & x_{4} = (1 / 2) a_{4} t^{2}; \end{matrix}

vagyis

\begin{matrix} a_{1} + 2 a_{2} + 2 a_{3} + a_{4} = 0. \end{matrix}

(16)

Az így kapott egyenletrendszer gyökei a keresett mennyiségek. A megoldás általános esetben nagyon hosszadalmas, de adott számadatokkal egyszerű. Annyi rögtön látszik, hogy

\begin{matrix} K_{1} = K_{2} = K_{3} = K_{7} = K_{8} = K_{4} / 2, \end{matrix}

valamint a (14), (15) és (16) egyenletek szerint valamennyi gyorsulás nem lehet azonos előjelű, mindig lesz olyan test, amelyik lefelé és olyan is, amelyik fölfelé mozog.

Blahó Ágnes (Szeged, Radnóti M. Gimn., II. o. t.)