Kezdőlap


Feladat:	897. fizika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Forgó Ignác , Gyimesi Ferenc , Hegyi György , Magyar András , Varga Zsuzsanna
Füzet:	1970/december, 236 - 237. oldal		PDF \| MathML
Témakör(ök):	Egyéb fénytörés, Geometriai szerkesztések alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1970/február: 897. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A beeső fénysugár és a beesési merőleges síkja mindig tartalmazza a gömb középpontját, ezért a gömböt $r$ sugarú körlappal helyettesítve síkban vizsgálhatjuk a problémát.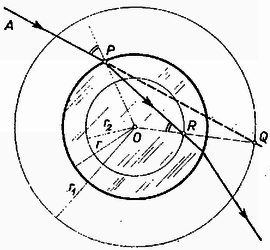

1. ábra

Vegyük észre, hogy a

P O R

és

P O Q

háromszögek hasonlók, mert megegyezik a két oldal aránya és a közbezárt szög. Ebből következik, hogy az

O R P ∢

egyenlő a beesési szöggel. Ugyanennek a háromszögnek a másik szöge,

O P R ∢

adja a törési szöget. A szinusz tétel alapján: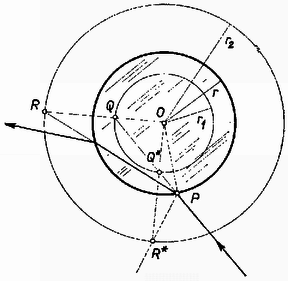

\begin{matrix} \frac{sin O R P ∢}{sin O P R ∢} = \frac{O P}{O R} = n . \end{matrix}

Mivel a Snellius‐Descartes-törvény szerint pontosan ilyen összefüggés van a beesési és a törési szögek között, ezért

n \geq 1

esetén (1. ábra) valóban helyes a fenti, eredetileg Weierstrasstól származó szerkesztés.

2. ábra

n < 1

esetén (2. ábra) szintén felvehető az

r_{1}

és

r_{2}

sugarú kör (most

r_{1} < r < r_{2})

. Ekkor, ha a beeső fénysugár meghosszabbítása metszi az

r_{1}

sugarú kört, a távolabbi metszéspontot

Q

-val jelölve, az

O Q

egyenes megadja

R

-t, és a

P R

egyenesnek az

r

sugarú gömbbe eső része pedig a megtört sugár útját. A bizonyítás ugyanazon háromszögek hasonlóságán alapul, mint az

n > 1

esetben.

n \geq 1

esetén a szerkesztés mindig elvégezhető,

n < 1

esetén azonban csak akkor, ha a beeső fénysugár legalább érinti az

r_{1}

sugarú kört. Ennél nagyobb beesési szögek esetén teljes visszaverődés lép fel.

Forgó Ignác (Győr, Mayer L. Gimn., IV. o. t. )

Megjegyzés:

n < 1

esetén nyilvánvaló, hogy a

P

-hez közelebbi

Q^{*}

pont nem felelhet meg, ugyanis ekkora törési szög

90^{\circ}

-nál nagyobbnak adódik. Ennek ellenére a bizonyítást ekkor is el lehet végezni, és az adódik, hogy

\begin{matrix} \frac{sin O R^{*} P ∢}{sin O P R^{*} ∢} = n . \end{matrix}

Vagyis most is teljesülni látszik a Snellius‐Descartes-törvény. Ennek azonban pusztán matematikai oka van, mert a törési szög mellékszögének szinusza megegyezik magának a szögnek a szinuszával. Ezért a Snellius‐Descartes-törvény precíz megfogalmazásába be kell venni azt az egyébként magától értetődő feltételt, hogy mind a törési, mind pedig a beesési szög hegyesszög. Minthogy a

Q^{*}

esetén a törési szög mellékszögét kapjuk, ez mindjárt rámutat azon megoldók állításának a tarthatatlanságára, akik szerint ez a második megoldás ,,a fénysugár visszavert részének az irányát'' adja, hiszen ez a ,,visszaverődési szög'', mivel éppen a valódi törési szöggel egyenlő, mindig nagyobb a beesési szögnél.