Kezdőlap


Feladat:	896. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Fridler Ferenc
Füzet:	1970/december, 234 - 236. oldal		PDF \| MathML
Témakör(ök):	Hatásos teljesítmény, Egyéb váltóáramú áramkörök, Feladat
Hivatkozás(ok):	Feladatok: 1970/február: 896. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vizsgáljuk az áramkört tetszőleges $t$ időpontban, és írjuk fel rá Kirchhoff törvényeit! (Az $U_{1} = 15$ V, $U_{2} = 10$ V, $R_{1} = 100$ ohm, $R_{2} = 150$ ohm $R_{3} = 50$ ohm, $φ = 60^{\circ}$ jelöléseket alkalmazzuk.)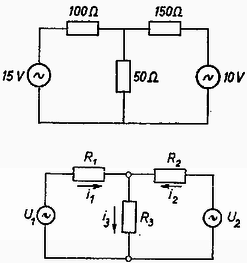

\begin{matrix} i_{1} R_{1} + i_{3} R_{3} = \sqrt[]{2} \cdot U_{1} \cdot sin ω t, \\ i_{2} R_{2} + i_{3} R_{3} = \sqrt[]{2} \cdot U_{2} \cdot sin (ω t + φ), \\ i_{1} + i_{2} - i_{3} = 0. \end{matrix}

Felhasználtuk, hogy egy

U

effektív értékű szinuszosan váltakozó feszültség maximális értéke

\sqrt[]{2} \cdot U

. Megoldva az egyenletrendszert:

\begin{matrix} i_{3} = \sqrt[]{2} \frac{R_{1} U_{2} sin (ω t + φ) + R_{2} U_{1} sin ω t}{R_{1} R_{2} + R_{2} R_{3} + R_{1} R_{3}} \end{matrix}

tehát az

R_{3}

ellenálláson folyó áram két különböző amplitúdójú és fázishelyzetű, azonos frekvenciájú, szinuszosan váltakozó mennyiség összege.
Az időegység alatt fejlődő hő kiszámítható a

P (t) = i_{3}^{2} R_{3}

függvény integrálásával, egyszerűbb azonban, ha felhasználjuk, hogy jelen esetben az áram

\begin{matrix} i_{3} = \sqrt[]{2} \cdot I \cdot sin (ω t + δ) \end{matrix}

alakban írható. A felírás jogosságát általános esetre bizonyítjuk.
Keressük

B

és

δ

olyan értékét, amelynél bármely időpontban igaz a

\begin{matrix} B sin (ω t + δ) = A_{1} sin (ω t + φ_{1}) + A_{2} sin (ω t + φ_{2}) \end{matrix}

egyenlőség. Trigonometrikus átalakítás és a megfelelő összevonás után

\begin{matrix} B cos δ sin ω t + B sin δ cos ω t = (A_{1} cos φ_{1} + A_{2} cos φ_{2}) sin ω t + (A_{1} sin φ_{1} + A_{2} sin φ_{2}) cos ω t . \end{matrix}

Ez csak akkor lehet igaz minden

t

-re, ha

\begin{matrix} B cos δ & = A_{1} cos φ_{1} + A_{2} cos φ_{2}, \\ B sin δ & = A_{1} sin φ_{1} + A_{2} sin φ_{2}, \end{matrix}

tehát kétismeretlenes egyenletrendszert kapunk. Megoldása (amely mindig létezik):

\begin{matrix} B = \sqrt[]{{(A_{1} sin φ_{1} + A_{2} sin φ_{2})}^{2} + {(A_{1} cos φ_{1} + A_{2} cos φ_{2})}^{2}} = \\ = \sqrt[]{A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} cos (φ_{1} - φ_{2})}, \\ tg δ = \frac{A_{1} sin φ_{1} + A_{2} sin φ_{2}}{A_{1} cos φ_{1} + A_{2} cos φ_{2}} . \end{matrix}

A váltakozó áramokat azért szemléltetik nagyon gyakran vektorokkal, mert ‐ mint azt fentebb bizonyítottuk ‐ maximális értékük és fázisszögük az összegezés során a vektorok nagyságához, illetve egy adott iránnyal bezárt szögéhez hasonló módon viselkedik.
Ennek alapján az

R_{3}

ellenálláson folyó szinuszosan váltakozó áram effektív értékének négyzete:

\begin{matrix} i^{2} = \frac{R_{1}^{2} U_{2}^{2} + 2 R_{2}^{2} U_{1}^{2} + 2 R_{1} R_{2} U_{1} U_{2} cos φ}{{(R_{1} R_{2} + R_{1} R_{3} + R_{2} R_{3})}^{2}} . \end{matrix}

Az időegység alatt fejlődő hő:

\begin{matrix} P = i^{2} R_{3} = \frac{R_{1}^{2} U_{2}^{2} + R_{2}^{2} U_{1}^{2} + 2 R_{1} R_{2} U_{1} U_{2} cos φ}{{(R_{1} R_{2} + R_{2} R_{3} + R_{1} R_{3})}^{2}} R_{3}, \end{matrix}

adatainkkal:

P = 0, 55 W = 0, 13 cal/s

.
A végeredmény csak akkor egyértelmű, ha az időegység elején és végén a feszültségek fázishelyzete ugyanolyan

(T = \frac{2 π}{ω}

az időegység egész számú többszöröse), vagy pedig a frekvencia olyan nagy, hogy a fáziseltérésből adódó különbség kicsi.

Fridler Ferenc (Veszprém, Lovassy L. Gimn., III. o. t. )