Feladat: 894. fizika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Dombi Gábor ,  Klebniczki József ,  Petz Dénes ,  Sailer Kornél ,  Varga Zsuzsanna 
Füzet: 1970/december, 230 - 232. oldal  PDF  |  MathML 
Témakör(ök): Egyenesvonalú mozgás lejtőn, Rugalmatlan ütközések, Ütközés fallal, Feladat
Hivatkozás(ok):Feladatok: 1970/február: 894. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A golyó a lejtőn forgás nélkül egyenletesen gyorsul és h függőleges elmozdulás után v=2gh sebességgel érkezik a lejtő aljába. Itt a lejtővel és a fallal egyszerre érintkezik, ezekkel bonyolult kölcsönhatásba lép és végül valamilyen irányba kirepül a lejtő és a fal szögletéből. A továbbiakban feltesszük, hogy ez a bonyolult kölcsönhatás lebontható független ütközések sorozatára, vagyis a golyó úgy verődik vissza a falról, mintha a lejtő nem lenne ott, majd az így szerzett sebességgel a lejtőnek ütközik stb. (A feltevés jogosságát ellenőrizhetjük egy olyan számítással, melyben a golyót erős rugókkal összekapcsolt tömegpontoknak tekintjük, és az ütközés lefolyását pontról pontra nyomon követjük.)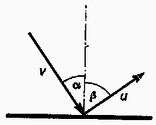

 
 
1. ábra
 

Határozzuk meg az egyes ütközések jellemző adatait! Ha egy v sebességű golyó α szöggel érkezik egy visszaverő felülethez (1. ábra) és az ütközési szám ε, akkor a β visszaverődési szöget és az ütközés utáni u sebességet a következő jellemzi. A felülettel párhuzamos sebességkomponens változatlan marad:
vsinα=usinβ.
A felületre merőleges komponens ε-szorosára változik:
εvcosα=ucosβ.
A fenti egyenletekből látható, hogy
1εtgα=tgβ.(1)
A megváltozott sebesség, u=vsin2α+ε2cos2α láthatóan függ v-n és ε-on kívül a beesési szögtől is.
 
 
2. ábra
 

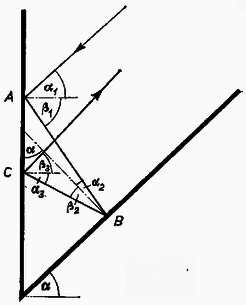A fentiek alapján az ütközés lefolyása a 2. ábrán láthatóhoz hasonló. A golyó felváltva ütközik a fallal és a lejtővel mindaddig, amíg valamelyik ütközés utáni sebesség vízszintessel bezárt szöge α és 90∘ közé nem esik. Ezután a ferde hajítás egyenletei szabják meg a golyó mozgását. Az egyes ütközések közti szakaszok (pl. AB, BC) nem a golyó tényleges elmozdulását, hanem csak a sebesség irányát jelzik. Mindegyik ütközésnél érvényes az (1) összefüggés, tehát
tgβi=1εtgαi,(2)
valamint a visszaverődés szöge és a következő ütközés beesési szöge közti geometriai feltétel:
αi+1=αi+β-90∘.(3)
Ezekből az egyenletekből α1=α kezdeti feltétel felhasználásával sorra kiszámíthatók az ütközési szögek.
Ha ε=1, akkor (2) alapján βi=αi. Ilyenkor egyszerűbben is megkaphatjuk az ütközések számát és a kirepülés szögét, ha felismerjük az analógiát a síktükrön visszaverődő fénysugár és a feladatban szereplő golyó mozgása között. Tükrözzük a fal a síkjára a lejtő b síkját, majd a b' tükörképre az a síkot stb. (3. ábra).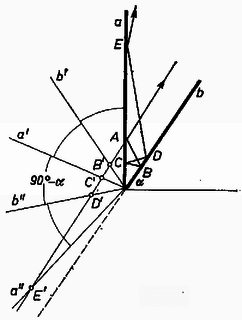
 
 
3. ábra
 

A tükörképeken az A, B', C', D' pontok egy egyenesen helyezkednek el.
Vezessük be valamely x szám egész részének jelölésére az [x] jelet! Az ábráról leolvashatjuk, hogy ha n=[180∘90∘-α] páros szám, akkor a kirepülő golyó a lejtő síkjával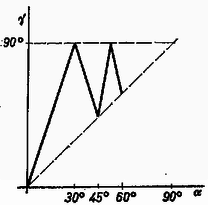
[180∘-180∘90∘-α](90∘-α),
páratlan n-re pedig
[180∘90∘-α](90∘-α)-90∘-α
szöget zár be. Ha ábrázoljuk a kirepülő golyó sebességének vízszintessel bezárt szögét α függvényében, akkor a 4. ábrán látható grafikont kapjuk.
 
 
4. ábra
 

Valahányszor 180∘90∘-α egész szám, vagyis
α=90∘-180∘m,m=3,4,5,...,
akkor a függvénynek töréspontjai vannak, ezekben a pontokban felváltva veszi fel a 90∘ és az α értéket. A kirepülés sebessége mindig megegyezik v-vel.
Ha ε≠1, akkor a fenti gondolatmenet nem alkalmazható, hanem (2) és (3)-ból kell számolni az ütközési szögeket. A rugalmas ütközés tárgyalásánál látott kritikus szögek megfelelőit itt is kiszámíthatjuk. A két és a három ütközést elválasztó határesetben a golyó a fallal párhuzamosan függőlegesen felfelé repül ki. Ez annak fele] meg, hogy α3=90∘. Ez viszont
tgα=εε2+ε+1
esetben teljesül. ε=1 esetben visszakapjuk a már meghatározott α=30∘ értéket, ε=0,5-re pedig α=28,1∘-ot kapunk. Hasonló módon számítható, hogy α=41,8∘-nál a golyó háromszor ütközik és a lejtővel párhuzamosan verődik vissza.
 

Klebniczki József (Szeged, Ságvári E. Gimn., III. o. t. )

és Petz Dénes (Bp., Veres Pálné Gimn., III. o. t. )
 

Megjegyzések. 1. Miután a golyó elhagyta a szögletet, bizonyos magasságig felrepül. Ez a magasság még ε=1 esetben sem egyezik meg az indítási magassággal (mint azt több megoldó az energiatételre való hivatkozással állította, mert a golyónak a pálya tetőpontján mozgási energiája is van) (kivéve azt a két speciális esetet, mikor a golyó valamelyik felülettel párhuzamosan verődik vissza).
2. Abszolút rugalmas golyó esetén 45∘-nál kisebb hajlásszögeknél egyszer ütközik a lejtővel és ezután ferde hajítás jön létre. 45∘-nál pontosan visszacsúszik a lejtőn, 45∘-nál nagyobb szögeknél többszöri visszaverődés után repül ismét ki a szögletből. Ha súrlódás is van, vagy nem abszolút rugalmas a golyó, már 45∘-nál kevéssel nagyobb szögek esetén is, ,,beragad'' a szögletbe.