Kezdőlap


Feladat:	873. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Hadik Róbert , Iglói Ferenc , Keresztúri András , Klebniczki József , Mihály György , Sailer Kornél
Füzet:	1970/október, 91 - 92. oldal		PDF \| MathML
Témakör(ök):	Pontrendszerek mozgásegyenletei, Nyomóerő, kötélerő, Munkatétel, energiamegmaradás pontrendszerekre, Egyenletesen gyorsuló rendszerek, Feladat
Hivatkozás(ok):	Feladatok: 1969/november: 873. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Írjuk föl a mozgásegyenleteket mindhárom kocsira, $A$ -nál a függőleges és vízszintes komponensekre egyaránt (1. ábra).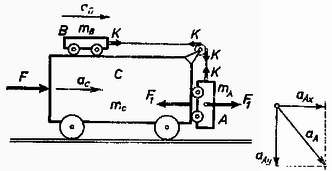

1. ábra

Tételezzük fel, hogy

a_{C} \geq 0

, így az

A

kocsi érintkezik

C

-vel, és köztük

F_{1} \geq 0

erő lép fel.

\begin{matrix} m_{A} a_{A x} = F_{1}, m_{A} a_{A y} = m_{A} g - K, m_{B} a_{B} = K, m_{C} a_{C} = F - F_{1} - K . \end{matrix}

A

és

C

kocsi érintkezéséből következő kényszerfeltétel

\begin{matrix} a_{A} x = a_{C} . \end{matrix}

A fonal nyújthatatlanságából következik, hogy a rendszert elmozdítva

\begin{matrix} Δ x_{B} = Δ x_{C} + Δ y_{A}, \\ a_{B} \frac{t^{2}}{2} = a_{C} \frac{t^{2}}{2} + a_{A y} \frac{t^{2}}{2}, \\ a_{B} = a_{C} + a_{A y} . \end{matrix}

Az egyenletrendszert megoldva

\begin{matrix} a_{A x} = a_{C} = \frac{(m_{A} + m_{B}) F - m_{A} m_{B} g}{(m_{A} + m_{B}) (m_{A} + m_{C}) + m_{A} m_{B}}, \\ a_{A y} = \frac{(m_{A} + m_{B} + m_{C}) m_{A} g - m_{B} F}{(m_{A} + m_{B}) (m_{A} + m_{C}) + m_{A} m_{B}}, \\ a_{B} = \frac{[(m_{A} + m_{C}) g + F] m_{A}}{m_{A} + m_{B}) (m_{A} + m_{C}) + (m_{A} + m_{B})} . \end{matrix}

Numerikus adatokkal:

a_{A x} = a_{C} = 3, 27 {m / s}^{2}

a_{A y} = 4, 57 {m / s}^{2}

a_{B} = 7, 84 {m / s}^{2}

. Az

A

kocsi eredő gyorsulása

a_{B} = \sqrt[]{a_{A x}^{2} + a_{A y}^{2}} = 5, 63 {m / s}^{2}

vízszintessel bezárt szöge

tg α = \frac{a_{A y}}{a_{A x}}

, ahonnan

α = 54, 50^{\circ}

Sailer Kornél (Ózd, József A. Gimn., IV. o. t.)

Megjegyzés. Egyenletrendszerünket azzal a feltételezéssel írtuk fel, hogy

A

és

C

kocsi érintkezik egymással, tehát

a_{C} \geq 0

. Ennek feltétele a megoldás felhasználásával

\begin{matrix} F \geq \frac{m_{A} m_{B} g}{m_{A} + m_{B}} . \end{matrix}

Numerikus adataink eleget tesznek ennek a feltételnek, így megoldásunk helyes volt.

A

és

B

kocsi akkor nem mozdul el

C

-hez viszonyítva, ha

a_{A y} = 0

, vagyis

\begin{matrix} F = (m_{A} + m_{B} + m_{C}) \frac{m_{A}}{m_{B}} g . \end{matrix}

F

ennél nagyobb, akkor felfelé, ha kisebb, lefelé mozdul el

A

.
Érdekes még megvizsgálni

A

eredő gyorsulásának nagyság és irány szerinti változását. Ehhez ábrázoljuk az

a_{A x} = f (a_{A y})

függvényt az

F

paraméter kiküszöbölésével. Ennek egyenlete

\begin{matrix} a_{A x} = \frac{m_{A}}{m_{B}} g - \frac{m_{A} + m_{B}}{m_{B}} a_{A y}, \end{matrix}

tehát a függvény képe egy egyenes.
A kocsi gyorsulását nagyság és irány szerint (2. ábra) megadja az egyenes valamely pontjának helyvektora.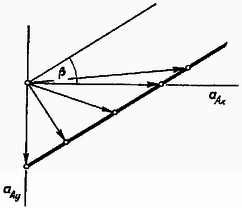

2. ábra

Innen közvetlenül leolvashatók a gyorsulások értékei abban az esetben, ha

C

áll

(a_{A x} = 0)

, vagy

A

és

B

áll

C

-hez viszonyítva

(a_{A y} = 0

. Ha

F

\frac{m_{A} m_{B} g}{m_{A} + m_{B}}

értéktől kiindulva nő, akkor

a_{A}

végpontja végigfut az egyenesen.

a_{A}

-nak a vízszintessel bezárt szöge

F

növelésével

β

-hoz tart, de mindig kisebb

β

-nál.

Kereszturi András (Bp., Eötvös J. Gimn., IV. o. t.)

II. megoldás. Megoldható a feladat az energiamegmaradás tételének felhasználásával is. Ugyanis álló helyzetből

t

ideig gyorsítva a rendszert az energiamegmaradás tétele szerint

\begin{matrix} \frac{1}{2} m_{A} v_{A}^{2} + \frac{1}{2} m_{B} v_{B}^{2} + \frac{1}{2} m_{C} v_{C}^{2} = F s_{C} + m_{A} g s_{A}, \end{matrix}

v = a t

és

s = a t^{2} / 2

összefüggés felhasználásával

\begin{matrix} \frac{1}{2} m_{A} {(\sqrt[]{a_{A x}^{2} + a_{A y}^{2}} t)}^{2} + \frac{1}{2} m_{B} {(a_{B} t)}^{2} + \frac{1}{2} m_{C} {(a_{C} t)}^{2} = F \cdot \frac{1}{2} a_{C} t^{2} + m_{A} g \frac{1}{2} a_{A y} t^{2} . \\ m_{A} (a_{A x}^{2} + a_{A y}^{2}) + m_{B} a_{B}^{2} + m_{C} a_{C}^{2} = F a_{C} + m_{A} g a_{A y} . & (1) \end{matrix}

C

-hez rögzített, tehát

a_{C}

-vel gyorsuló koordináta-rendszerben minden

m

tömegre

- m a_{C}

erő hat, így az energiamegmaradás törvénye

\begin{matrix} \frac{1}{2} m_{A} {(a_{A y} t)}^{2} + \frac{1}{2} m_{B} {[(a_{B} - a_{C}) t]}^{2} = (m_{A} g - m_{B} a_{C}) \frac{1}{2} a_{A y} t^{2}, \\ m_{A} a_{A y}^{2} + m_{B} {(a_{B} - a_{C})}^{2} = (m_{A} g - m_{B} a_{C}) a_{A y} . & (2) \end{matrix}

A kényszerfeltételek hozzávételével az (1), (2) egyenletrendszer megoldható.
Ez a megoldás nemcsak az energiamegmaradás törvényét, hanem a tehetetlenségi erő fölvételével Newton II. törvényét is fölhasználja, előnye mégis az, hogy a kényszererők nem végeznek munkát, így ezekkel nem kell számolunk.

Mihály György (Bp., Kölcsey F. Gimn., IV. o. t.)

Megjegyzés. A legtöbb dolgozat azért nem nyert pontot, mert szerzőjük a 3 testből álló rendszerre egyetlen mozgásegyenletet írt fel. Newton II. törvényét minden egyes testre külön-külön kell alkalmaznunk.