Kezdőlap


Feladat:	861. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Berkes Enikő , Czigler Ágoston , Gál Péter , Simon László
Füzet:	1970/május, 228 - 229. oldal		PDF \| MathML
Témakör(ök):	Merev test egyensúlya, Feladat
Hivatkozás(ok):	Feladatok: 1969/október: 861. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A súlyerő, a kötélerő és a két felület által kifejtett kényszererők hatásvonalai a henger tengelyén mennek át. A rendszer nyugalomban van, tehát a négy erő eredője 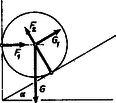$0$ .

Írjuk ezt fel a vízszintes és függőleges összetevőkre külön-külön:

\begin{matrix} F_{2} \cdot sin α - G_{1} \cdot cos α = F_{1}, \\ F_{2} \cdot cos α + G_{1} \cdot sin α = G . \end{matrix}

Mivel

G = 8 kp

G_{1} = 3 kp

és

α = 30^{\circ}

, a 2. egyenletből, majd az 1. egyenletből

\begin{matrix} F_{2} = \frac{G - G_{1} \cdot sin α}{cos α} = \frac{8 kp - 3 kp \cdot 0, 5}{\sqrt[]{3 / 2}} = \frac{13}{\sqrt[]{3}} kp \approx 7, 5 kp; \\ F_{1} = \frac{13}{\sqrt[]{3}} \cdot 0, 5 kp - 3 \cdot \frac{\sqrt[]{3}}{2} kp = \frac{2 \sqrt[]{3}}{3} kp \approx 1, 15 kp . \end{matrix}

Simon László (Szeged, Ságvári E. Gimn., II. o. t.)

II. megoldás. Mivel a golyó nyugalomban van, bármely pontra a forgatónyomatékoknak egyensúlyban kell lenniük. A golyó és a lejtő érintkezési pontjára (alkotójára) nézve:

\begin{matrix} r \cdot G_{1} + F_{1} \cdot r \cdot cos α = r \cdot G \cdot sin α . \end{matrix}

A golyó és a fal érintkezési pontjára nézve:

\begin{matrix} G_{1} \cdot r \cdot sin α + F_{2} \cdot r \cdot cos α = G \cdot r . \end{matrix}

A két egyenletből

r

kiesik,

F_{1}

és

F_{2}

meghatározható:

\begin{matrix} F_{1} = \frac{G \cdot sin α - G_{1}}{cos α}, illetve F_{2} = \frac{G - G_{1} sin α}{cos α} . \end{matrix}

Numerikusan

F_{1} = 2 / \sqrt[]{3} kp

; és

F_{2} = 13 / \sqrt[]{3} kp

Gál Péter (Bp., Fazekas M. Gyak., Gimn., II. o. t.)