Kezdőlap


Feladat:	860. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Gács Lajos , Herényi Levente
Füzet:	1970/április, 185 - 190. oldal		PDF \| MathML
Témakör(ök):	Erők forgatónyomatéka, Erőrendszer eredője, Feladat
Hivatkozás(ok):	Feladatok: 1969/október: 860. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladatot úgy fogjuk megoldani, hogy a vizsgált szerkezetet képzeletben részekre bontjuk és minden részre külön-külön felírjuk a nyugalom feltételét:

\begin{matrix} a ható erők összege 0, \\ a forgatónyomatékok összege 0. \end{matrix}

A rendszert annyi darabra bontjuk szét, hogy végül a megoldáshoz elég egyenlet álljon rendelkezésünkre.
Először bebizonyítjuk, hogy ha egy merev rúd valamely keresztmetszetében valamilyen ‐ tetszőleges irányú ‐

F

erő hat, akkor ugyanez az erő feszíti a rúd minden keresztmetszetét addig, amíg a rúdra külső erő nem hat.
Nézzük a rúd egy kis darabját! Feltételezésünk szerint erre a darabra csak a rúd jobb és bal oldali folytatása hat. Ha az egyik végén (pl. a bal oldalin) a bal oldali rész

K

erővel hat a darabra, akkor ahhoz, hogy a darab nyugalomban maradjon, másik végén ellentétes irányú, azonos nagyságú erőnek kell hatnia, mert a ható erők összege 0. Ha a rúd jobb oldali része a vizsgált darabra

K

erővel hat, akkor a vizsgált darab a rúd jobb oldali részére ellentétes irányú, azonos nagyságú erővel (hatás-ellenhatás törvénye), azaz

K

-val hat. Beláttuk, hogy ha a rúd bal oldali része

K

erővel hat a rúd egy darabjára, akkor ez a darab a

K

erőt továbbítja a rúd jobb oldali része felé.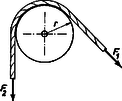

1. ábra

Írjuk fel a csigára ható forgatónyomatékok összegét (1. ábra):

\begin{matrix} M = F_{1} r - F_{2} r = 0. \end{matrix}

Ebből

F_{1} = F_{2}

, azaz kijelenthetjük, hogy ha valahol a kötél irányt változtat, akkor a csigára két egyenlő nagyságú kötélerő hat.
Az előbbi gondolatmenethez hasonló módon azt is bebizonyíthatjuk, hogy ezen erők nagysága

G

(ha

G = 150 kp

, a kötélre akasztott test súlya). A kötélben ható erő azért mindig kötélirányú, mert a kötél ‐ ellentétben a merev rúddal ‐ forgatónyomaték hatására elgörbül.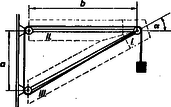

2. ábra

a) A konzol szaggatott vonallal határolt részeit (2. ábra) külön vizsgáljuk.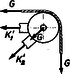

3. ábra

Az egyensúly feltétele az I. részre (3. ábra; a vízszintes rúdban ható erőt

K_{1}

-gyel, a ferde rúdban hatót

K_{2}

-vel, a reakcióerőket

K'_{1}

K'_{2}

-vel, a függőleges, illetve vízszintes komponenseket ‐ melyeket az ábrán nem tüntettünk fel ‐

y

, illetve

x

indexszel jelöljük):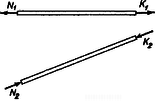

\begin{matrix} K'_{2 x} - K'_{1 x} - G - G cos α = 0, \end{matrix}

a

)

\begin{matrix} K'_{2 y} - K'_{1 y} - G - G sin α = 0. \end{matrix}

b

)

4. ábra

A II. és III. részre (4. ábra):

\begin{matrix} K_{1 y} \cdot b = 0, \end{matrix}

(II)

\begin{matrix} K_{2 x} \cdot a - K_{2 y} \cdot b = 0. \end{matrix}

(III)

Az I. egyenletcsoportnál nem kellett felhasználni a forgatónyomatékok összegét, a II. és III.-nál az erők összegét.
Tudjuk, hogy

K_{1}

K'_{1}

, valamint

K_{2}

K'_{2}

egymás reakcióerői, ezért

\begin{matrix} K_{1 x} = K'_{1 x}, K_{1 y} = K'_{1 y}, K_{2 x} = K'_{2 x}, K_{2 y} = K'_{2 y} . \end{matrix}

A II. és III. egyenletekből következik, hogy a

K_{1}

és

K_{2}

erő a rúd irányában hat.
Az egyenletrendszer megoldva

\begin{matrix} K_{1 x} & = G (\frac{b}{a} - 1) = 110 kp, & K_{1 y} = 0, \\ K_{2 x} & = G (\frac{b}{a} + cos α) = 390 kp, & K_{2 y} = G (1 + sin α) = 215 kp . \end{matrix}

Ezzel a rudakban ható erőket teljesen meghatároztuk. Célszerű kiszámítani az erők nagyságát és irányát is:

\begin{matrix} K_{1} = G (\frac{b}{a} - 1) = 110 kp & α_{1} = 0^{\circ}, \\ K_{2} = G (1 + sin α) \sqrt[]{\frac{b^{2}}{a^{2}} + 1} = 450 kp, & α_{2} = 210^{\circ} . \end{matrix}

(

α_{1} α_{2}

az erők vízszintessel bezárt szöge, az óramutató járásával ellentétes irányban mérve.)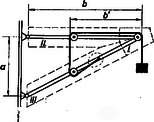

5. ábra

b) Az előzőhöz hasonló felbontást alkalmazva (5. ábra) ismét felrajzoljuk a megfelelő részekre ható erőket (6., 7. ábra), és felírjuk az egyensúly feltételét.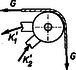

6. ábra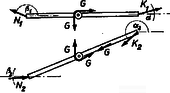

7. ábra

\begin{matrix} K'_{2 x} - K'_{1 x} - G = 0, \end{matrix}

a

)

\begin{matrix} K'_{2 y} - K'_{1 y} - G = 0, \end{matrix}

b

)

\begin{matrix} - N_{1 x} + G + K_{1 x} = 0, \end{matrix}

(II

a

)

\begin{matrix} N_{1 y} - G + K_{1 y} = 0, \end{matrix}

(II

b

)

\begin{matrix} - N_{1 y} \cdot b + G \cdot b' = 0, \end{matrix}

(II

c

)

\begin{matrix} N_{2 x} + G cos α - G cos α - K_{2 x} = 0, \end{matrix}

(III

a

)

\begin{matrix} N_{2 y} = G + G sin α - G sin α - K_{2 y} = 0, \end{matrix}

(III

b

)

\begin{matrix} - N_{2 y} \cdot b + N_{2 x} \cdot a - G \cdot b' = 0. \end{matrix}

(III

c

)

Továbbá

K_{1 x} = K'_{1 x}, K_{1 y} = K'_{1 y}, K_{2 x} = K'_{2 x}, K_{2 y} = K'_{2 y} .

Az egyenletrendszert megoldva azt kapjuk, hogy a vízszintes rúdban a két csiga közötti részen

\begin{matrix} K_{1 x} = G (\frac{b}{a} - 1) = 110 kp, & K_{1 y} = G (1 - \frac{b'}{b}) = 45 kp; \\ K_{1} = 118 kp & a_{1} = & 22^{\circ}, \end{matrix}

a középső csiga és a fal között

\begin{matrix} N_{1 x} - G \frac{b}{a} = 260 kp, & N_{1 y} = G \frac{b'}{b} = 105 kp; \\ N_{1} = 280 kp, & β_{1} = 158^{\circ} & nagyságú és irányú erő hat. \end{matrix}

A ferde rúdban a végén levő csiga és a kötél vége közötti részen

\begin{matrix} K_{2 x} = G \frac{b}{a} = 260 kp, & K_{2 y} - G (2 - \frac{b'}{b}) = 195 kp; \\ K_{2} = 325 kp, & α = & 217^{\circ}, \end{matrix}

a középső csiga és a fal között

\begin{matrix} N_{2 x} = G \frac{b}{a} = 260 kp, & N_{2 y} - G (1 - \frac{b'}{b}) = 45 kp; \\ N_{2} = 264 kp, & β = 3^{\circ}, & nagyságú és irányú erő hat. \end{matrix}

Tisztázni kell még, hogy milyen erő hat a ferde rúdban a középső csiga és a kötél vége közötti részen.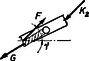

8. ábra

Vizsgáljuk a rúdnak az 5. ábrán bekarikázott részét (8. ábra):

\begin{matrix} F_{x} - G cos α - K_{2 x} = 0, \end{matrix}

\begin{matrix} F_{y} - G sin α - K_{2 y} = 0. \end{matrix}

Ebből a keresett erő:

\begin{matrix} F_{x} = G (\frac{b}{a} + cos α) = 390 kp, \\ F_{y} = G (2 - \frac{b'}{b} + sin α) = 270 kp; \\ F = 470 kp, γ = 34^{\circ} . \end{matrix}

c) Az előző két megoldáshoz hasonló módon járunk el. Természetesen, két azonos helyen ható, párhuzamos,

G

nagyságú erő helyettesíthető

2 G

-vel (9., 10. ábra).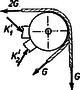

9. ábra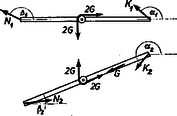

10. ábra

\begin{matrix} K'_{2 x} + K'_{1 x} - G cos α - 2 G = 0, \end{matrix}

a

)

\begin{matrix} K'_{2 y} - G \cdot sin α - G - K'_{1 y} = 0, \end{matrix}

b

)

\begin{matrix} - N_{1 x} + 2 G - K_{1 x} = 0, \end{matrix}

(II

a

)

\begin{matrix} N_{1 y} - 2 G + K_{1 x} = 0, \end{matrix}

(II

b

)

\begin{matrix} - N_{1 y} \cdot b + 2 G \cdot b' = 0, \end{matrix}

(II

c

)

\begin{matrix} N_{2 x} + 2 G cos α - G cos α - K_{2 x} = 0, \end{matrix}

(III

a

)

\begin{matrix} - N_{2 y} + 2 G + 2 G sin α - G sin α - K_{2 y} = 0, \end{matrix}

(III

b

)

\begin{matrix} - N_{2 y} \cdot b + 2 G \cdot b' - N_{2 x} \cdot a = 0. \end{matrix}

(III

c

)

Megoldva az egyenletrendszert, a ható erők a vízszintes rúdban a két csiga közötti részen:

\begin{matrix} K_{1 x} = G (2 - \frac{b}{a}) = 40 kp, & K_{1 y} = 2 G (1 - \frac{b'}{b}) = 90 kp; \\ K_{1} = 98, 5 kp, & α_{1} = & 109^{\circ}, \end{matrix}

a középső csiga és a fal közötti részen:

\begin{matrix} N_{1 x} = G \frac{b}{a} = 260 kp, & N_{1 y} = 2 G \frac{b'}{b} = 210 kp; \\ N_{1 x} = 334 kp, & β_{1} = & 141^{\circ}, \end{matrix}

a ferde rúdban a végén levő csiga és a kötél vége közötti részen:

\begin{matrix} K_{2 x} = G (\frac{b}{a} + cos α) = 390 kp, & K_{2 y} = G (3 - 2 \frac{b'}{b} + sin α) = 315 kp; \\ K_{2} = 500 kp, & α_{2} = & 219^{\circ}, \end{matrix}

a fal és a középső csiga közötti részen:

\begin{matrix} N_{2 x} = G \frac{b}{a} = 260 kp, & N_{2 y} = 2 (\frac{b'}{b} - 1) = 60 kp; \\ N_{2} = 267 kp, & β_{2} = & 13^{\circ}, \end{matrix}

A középső csiga és a kötél vége közötti részen ható erő meghatározásához vizsgáljuk a ferde rúd 5. ábrán bekarikázott részét (11. ábra):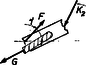

11. ábra

\begin{matrix} F_{x} - G cos α - K_{2 x} = 0, \\ F_{y} - G sin α - K_{2 y} = 0. \end{matrix}

Ebből

\begin{matrix} F_{x} = G (\frac{b}{a} + 2 cos α) = 520 kp, & F_{y} = G (3 - 2 \frac{b'}{b} + 2 sin α) = 390 kp; \\ F = 650 kp, & γ = & 37^{\circ}, \end{matrix}

Herényi Levente (Bp., I. István Gimn. II. o. t.)

Gács Lajos (Bp., Landler Jenő Techn., II. o. t.)

dolgozata alapján

Megjegyzések. 1. Ilyen jellegű feladatok megoldásánál ajánlatos részletes rajzot készíteni a ható erőkről. Az erők irányát szabadon választhatjuk, célszerű azonban ‐ a nagyobb szemléletesség kedvéért ‐ úgy megválasztani őket, hogy komponenseikre pozitív értéket kapjunk. Ezt tettük ennél a megoldásnál is.
2. Mint láthattuk, az a) feladat kivételével a rudakban ható erők sehol sem voltak rúdirányúak. Éppen ezért kaptak helytelen eredményt azok, akik ‐ minden indoklás nélkül ‐ a ható erőknek rúdirányú komponensekre való bontásával próbálták a feladatot megoldani.