Kezdőlap


Feladat:	855. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Gács Lajos , Hennyey Katalin , Horváth Zoltán , Iglói Ferenc , Szalay András
Füzet:	1970/március, 141 - 143. oldal		PDF \| MathML
Témakör(ök):	Egyéb merev test síkmozgások, Csúszó súrlódás, Tapadó súrlódás, Feladat
Hivatkozás(ok):	Feladatok: 1969/szeptember: 855. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A fonál elégetése előtt a rúdra $K$ kötélerő, a talaj $F$ nyomóereje és $m g$ súlyerő hat. A rúd nyugalomban van, ezért az erők eredője és a forgatónyomatékok összege nulla.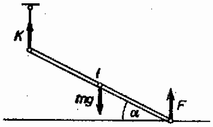

1. ábra

A talaj és a rúd közt fellépő

F

erő csak függőleges lehet, hiszen a másik két erő is függőleges (1. ábra), így

\begin{matrix} K + F - m g = 0, \frac{K \cdot l \cdot cos α}{2} - \frac{F \cdot l \cdot cos α}{2} = 0. \end{matrix}

Az egyenletrendszer megoldása (

α \neq 90^{\circ}

esetben)

K = F = m g / 2

.
Ha a fonalat elégetjük, akkor a rúd nem marad egyensúlyban, hanem gyorsuló mozgásba kezd. Mozgását jellemezhetjük a súlypont gyorsulásának vízszintes és függőleges összetevőjével, valamint a súlypont körüli

β

szöggyorsulással. A rúdra ható erők: az

m g

súlyerő, a talaj

F

nyomóereje és

S

súrlódási erő (2. ábra).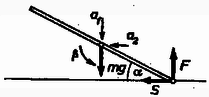

2. ábra

A talaj most nemcsak függőleges nyomóerővel hat a rúdra, mivel az nincs egyensúlyban, hanem vízszintes súrlódási erővel is, és éppen ez az erő hozza létre a rúd vízszintes gyorsulását.
Írjuk fel a mozgásegyenletet a függőleges és a vízszintes komponensekre

\begin{matrix} m g - F = m \cdot a_{1}, \end{matrix}

(1)

\begin{matrix} S = m a_{2} . \end{matrix}

(2)

Felírhatjuk még a forgómozgás alapegyenletét (a súlypontra vonatkoztatva), felhasználva, hogy egy homogén rúd tehetetlenségi nyomatéka

m l^{2} / 12

\begin{matrix} \frac{F \cdot l \cdot cos α}{2} - \frac{S \cdot l \cdot sin α}{2} = \frac{m l^{2}}{12} β . \end{matrix}

(3)

A test mozgását jellemző

a_{1}

a_{2}

és

β

mennyiségek nem függetlenek egymástól, mivel a rúd alsó vége csak vízszintes irányú mozgást végezhet. Ezt az

\begin{matrix} a_{1} = \frac{l \cdot β}{2} cos α \end{matrix}

(4)

egyenlet biztosítja.
Az (1)‐(4) egyenletekben

5

ismeretlen szerepel (

a_{1}

a_{2}

β

F

S

). A hiányzó ötödik egyenlet felírásánál két esetet kell megkülönböztetnünk. Ha a rúd talppontja csúszik a talajon, akkor

\begin{matrix} S = μ F . \end{matrix}

(5)

Ez az egyenlet akkor érvényes, ha a rúd valóban jobbra csúszik, vagyis ha

\begin{matrix} \frac{l}{2} β sin α ≧ a_{2} . \end{matrix}

(6)

Az (1)‐(5) egyenletrendszer megoldása

F

és

S

-re:

\begin{matrix} F = \frac{m g}{1 + 3 cos α (cos α - μ sin α)}, \end{matrix}

(7)

\begin{matrix} S = \frac{m g μ}{1 + 3 cos α (cos α - μ sin α)}; \end{matrix}

(8)

a (6) feltétel pedig akkor teljesül, ha

\begin{matrix} μ ≦ \frac{3 tg α}{1 + 4 {tg}^{2} α} . \end{matrix}

(9)

Ha a rúd nem csúszik a talajon, akkor

S

és

F

között már nem áll fenn az (5) egyenlet. A hiányzó egyenletet éppen az a feltétel adja, hogy a rúd talppontja nem mozdul el, vagyis

\begin{matrix} \frac{l}{2} β sin α = a_{2} . \end{matrix}

(5')

Ez a lehetőség akkor valósul meg, amikor a súrlódási együttható elég nagy ahhoz, hogy teljesüljön a

\begin{matrix} S ≦ μ F \end{matrix}

(6')

egyenlőtlenség. Az (1)‐(4) és

(5')

egyenletrendszer megoldása

\begin{matrix} F = m g (1 - \frac{3}{4} cos^{2} α), \end{matrix}

(7')

\begin{matrix} S = \frac{3}{4} m g sin α cos α, \end{matrix}

(8')

és a megoldás érvényességének

(6')

feltétele

\begin{matrix} μ ≧ \frac{3 tg α}{1 + 4 {tg}^{2} α} \end{matrix}

(9')

alakban írható.
Ábrázoljuk

F

és

S

erőket az indulás

α

szögének függvényében adott

μ

súrlódási együttható mellett. Először határozzuk meg azt a kritikus

α

szöget, melynél a rúd még éppen nem csúszik!
A

μ_{0} = \frac{3 tg α}{1 + 4 {tg}^{2} α}

egyenletnek

α

-ra nincs megoldása, ha

μ_{0} > 3 / 4

. Ilyenkor mindig

(9')

érvényes, vagyis a rúd nem csúszik. Ha

μ_{0} < 3 / 4

, akkor létezik olyan

α_{1}

és

α_{2}

szög, melyek közé választva az

α

indítási szöget, a rúd csúszni kezd. Amennyiben

α < α_{1}

vagy

α > α_{2}

, akkor

(9')

teljesül, és a rúd nem csúszik.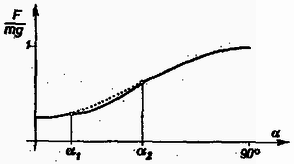

3. ábra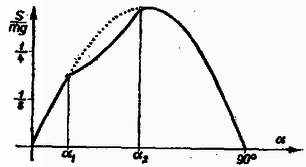

4. ábra

A 3. és 4. ábrán

F

és

S

különböző értékeit láthatjuk

μ_{0} = 3 / 5

esetén.

Gács Lajos (Bp., Landler J. Techn., II. o. t.) és

Hennyey Katalin (Bp., Kölcsey F. Gimn., III. o. t.)

dolgozata alapján