Kezdőlap


Feladat:	844. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ábrahám Zoltán , Soós Lajos , Zámolyi Ferenc
Füzet:	1970/március, 135 - 137. oldal		PDF \| MathML
Témakör(ök):	Összetartó erők eredője, Geometriai szerkesztések alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1969/május: 844. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A merev rúd egyensúlyának az a feltétele, hogy a rá ható eredő erő és az eredő forgatónyomaték nulla legyen. Ez csak akkor teljesülhet, ha a $G_{1}$ , $G_{2}$ és $Q$ súlyerők $G$ eredőjének és a $K_{1}$ , $K_{2}$ kötélerőknek a hatásvonala egy pontban metszi egymást.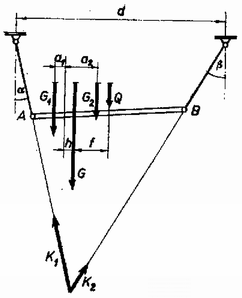
Ennek alapján a szerkesztéses megoldás könnyen adódik (1. ábra).

1. ábra

Először meghúzzuk a

K_{1}

K_{2}

hatásvonalának metszéspontján átmenő függőlegest, erre illeszkedik

G_{1}

G_{2}

és

Q

eredője,

G

. Megszerkesztjük

G_{1}

és

G_{2}

eredőjének az

f \cdot Q = h (G_{1} + G_{2})

feltételt kielégítő

h

távolságát

G

-től. Ezután a

h

-val jellemzett hatásvonal ellenkező oldalára

G_{1}

és

G_{2}

már sokféleképpen vehető fel, csak a

G_{1} a_{1} = G_{2} a_{2}

feltételt kell kielégíteni (s természetesen

G_{1}

G_{2}

-nek a rúdon kell maradnia). Ha

Q = 0

a szerkesztés egyszerűsödik.
A szerkesztésből látható, hogy

β

annál nagyobb, minél közelebb van

G

hatásvonala

A

-hoz. Ezért

β

akkor maximális, ha a

G_{1}

G_{2}

súlyokat

A

-ba helyezzük.

α

értéke akkor nulla, ha

s^{2} + d^{2} ≧ {(s + l)}^{2}

és a rúd súlytalan (2. ábra). Ha

s^{2} + d^{2} < {(s + l)}^{2}

, súlytalan rúd esetén a jobb oldali kötél a rúddal egy egyenesbe esik (3. ábra), s az így keletkezett háromszögből cosinus tétellel: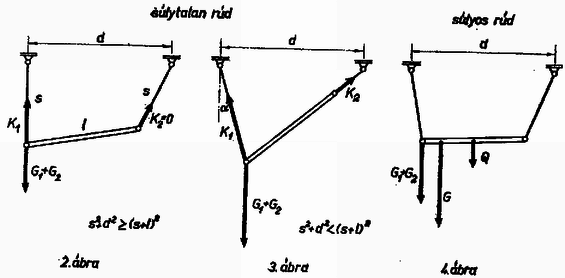

\begin{matrix} cos (90^{\circ} - α) = sin α = \frac{d^{2} - l^{2} - 2 l s}{2 d s} . \end{matrix}

Súlyos rúd esetén (4. ábra) az eredő

G

erő nem kerülhet

A

-ba, s így a jobb oldali kötél a rúddal nem alkot egy egyenest. A maximális

β

-hoz tartozó

α

ekkor is kiszámítható, de nehezebben (lásd a II. megoldást).

Zámolyi Ferenc (Budapest, Berzsenyi D. Gimn., II. o. t.)

II. megoldás. Felírjuk a merev rúd egyensúlyának feltételét kifejező egyenleteket (5. ábra):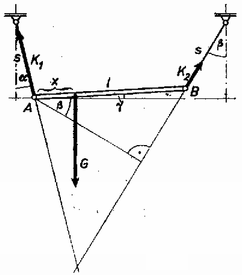

\begin{matrix} K_{1} sin α = K_{2} sin β, & (1) \\ K_{1} cos α + K_{2} cos β = G, & (2) \\ G x cos y - K_{2} l cos (β + y) = 0. & (3) \end{matrix}

5. ábra

Továbbá az ábráról

\begin{matrix} tg y = \frac{s (cos α - cos β)}{d - s (sin α + sin β)} . \end{matrix}

(4)

Az első két egyenletből

\begin{matrix} K_{2} = \frac{G}{ctg α \cdot sin β + cos β}, \end{matrix}

ezt a harmadikba helyettesítve kapjuk:

\begin{matrix} x = l [\frac{1}{tg β \cdot ctg α + 1} + \frac{cos β - cos α}{(ctg α + ctg β) (d / s - sin α - sin β)}] . \end{matrix}

Az így kapott támadáspont

2

oldalára az I. megoldásban kifejtett módon (tehát, hogy

G_{1}

G_{2}

Q

eredőjének hatásvonala a rudat

A

-tól a fenti

x

távolságra messe) lehet elhelyezni a súlyokat. Konkrét esetben elég

α

és

β

közül az egyiket megadni, mert fennáll közöttük a következő összefüggés:

\begin{matrix} s \cdot sin α + \sqrt[]{l^{2} - s^{2} {(cos α - cos β)}^{2}} + s \sqrt[]{1 - cos^{2} β} = d . \end{matrix}

(5)

Ez átrendezés és kétszeri négyzetre emelés után egy

cos β

-ban másodfokú egyenletre vezet, melyet adott

s

l

d

α

értékek esetén nem nehéz megoldani. A maximális

β

kérdését az első megoldáshoz hasonlóan tárgyalhatjuk, kiegészítve azzal, hogy súlyos rúd esetén is kiszámíthatjuk a maximális

β

-hoz tartozó

α

-t az (1)‐(5) egyenletek segítségével (

x = 0

-t helyettesítve).

Ábrahám Zoltán (Nagykőrös, Arany J. Gimn., II. o. t.)

Megjegyzés. A valóságban

s^{2} + d^{2} \geq {(s + l)}^{2}

esetén sem valósítható meg teljesen az

α = 0

helyzet, mert a jobb oldali kötél csak akkor feszes (s tetszőlegesen kis súlyú rúd esetén feszes), ha hat benne erő, s ezt az erőt csak függőleges erők (

K_{1}

G_{1} + G_{2}

) nem kompenzálhatják.