Kezdőlap


Feladat:	837. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Fischer Ágnes , Fittler Katalin , Nagy András , Szabó László
Füzet:	1970/március, 130 - 132. oldal		PDF \| MathML
Témakör(ök):	Összetartó erők eredője, A (mechanikai) feszültség, Hooke-törvény, Szélsőérték differenciálszámítással, Geometriai szerkesztések alkalmazása, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1969/április: 837. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Feltételezzük a következőket: a rúd vízszintes tengelyű csuklóval csatlakozik a falhoz, tehát a kötél megnyúlása és a lehajlás miatt nem lép fel a rúdban rugalmas erő, továbbá a lehajlás miatt fellépő szögváltozás elhanyagolható.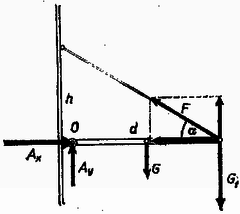

1. ábra

Az erő egyensúly-egyenletei (1. ábra)

\begin{matrix} A_{x} - F cos α = 0, \\ A_{y} + F sin α - G - G'_{1} = 0. \end{matrix}

A forgatónyomatékok egyensúlyegyenlete (O pontra):

\begin{matrix} G \cdot \frac{d}{2} + G_{1} \cdot d - F \cdot sin α \cdot d = 0 \end{matrix}

és

\begin{matrix} sin α = \frac{h}{\sqrt[]{h^{2} + d^{2}}} . \end{matrix}

Az egyenleteket megoldva

\begin{matrix} F = (\frac{G}{2} + G_{1}) \sqrt[]{1 + \frac{d^{2}}{h^{2}}} . \end{matrix}

A megnyúlás

\begin{matrix} λ = \frac{F \cdot l}{E \cdot q}, ahol \end{matrix}

l = \sqrt[]{d^{2} + h^{2}}

a kötél hossza és

q = r^{2} π

a keresztmetszete. Így

\begin{matrix} λ = \frac{\frac{G}{2} + G_{1}}{E \cdot q} \cdot \frac{h^{2} + d^{2}}{h} . \end{matrix}

A minimum helyen a függvény első differenciálhányadosa eltűnik.

λ = min

., ha

\begin{matrix} (\frac{h^{2} + d^{2}}{h})' = 1 - \frac{d^{2}}{h^{2}} = 0, azaz h = d . \end{matrix}

h = - d

érték fizikailag értelmetlen.)

\begin{matrix} λ_{min} = \frac{\frac{G}{2} + G_{1}}{E \cdot q} \cdot 2 d = 0, 278 mm \end{matrix}

és a minimális megnyúláshoz tartozó kötélerő

\begin{matrix} F = (\frac{G}{2} + G_{1}) \sqrt[]{2} = 24, 74 kp . \end{matrix}

Fittler Katalin (Mosonmagyaróvár, Kossuth Gimn., II. o. t.)

Szabó László (Győr, Révai M. Girnn., M. o. t.)

Megjegyzés. A minimum kiszámítása más módszerrel is történhet.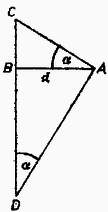

1. ábra

A 2. ábráról felírható

\begin{matrix} \frac{C A}{C D} = \frac{C B}{C A}, C D = y = \frac{C A^{2}}{C B} = \frac{h^{2} + d^{2}}{h} . \end{matrix}

y

szakaszt az

A

pont körül forgó derékszög két szára metszi ki a

d

távolságra fekvő egyenesből. Belátható, hogy

y

annál nagyobb, minél nagyobb

C B

és

D B

közül a nagyobbik.

y

akkor a legkisebb, amikor

C B

és

D B

közül a nagyobbik a legkisebb, tehát amikor egyenlők.

Fischer Ágnes (Bp. Móricz Zs. Gimn., III. o. t.)

Legyen

h = d + x

, ekkor belátható, hogy az

y = \frac{d^{2} + {(d + x)}^{2}}{d + x}

kifejezés minimuma

x = 0

-nál van. Ugyanis induljunk ki abból, hogy

x^{2} \geq 0

(az egyenlőség

x = 0

esetén áll fenn).
Mindkét oldalhoz adjunk

2 d^{2} + 2 d x

-et:

\begin{matrix} d^{2} + d^{2} + 2 d x + x^{2} \geq 2 d^{2} + 2 d x . \end{matrix}

Ezért

\begin{matrix} d^{2} + {(d + x)}^{2} \geq 2 d (d + x) . \end{matrix}

Mivel

h = d + x > 0

, írhatjuk, hogy

\begin{matrix} \frac{d^{2} + {(d + x)}^{2}}{d + x} \geq 2 d . \end{matrix}

Egyenlőség akkor van, ha

x = 0

, azaz ha

h = d

Nagy András (Budapest, Fazekas M. Gimn., II. o. t.)