Kezdőlap


Feladat:	825. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bajmóczy Ervin , Dalos Mihály , Maróti Péter , Szalai Gábor , Szöllősy Péter
Füzet:	1970/január, 34 - 37. oldal		PDF \| MathML
Témakör(ök):	Rögzített tengely körüli forgás (Merev testek kinematikája), Pillanatnyi forgástengely, Feladat
Hivatkozás(ok):	Feladatok: 1969/február: 825. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az $r_{2}$ sugarú "2'' fogaskerék mozgása két forgó mozgásból tevődik össze. Egyrészt $ω$ szögsebességgel forog az "1'' fogaskerék középpontja körül, másrészt pedig úgy forog a saját tengelye körül $ω_{2}$ szögsebességgel, hogy csúszásmentesen gördüljön végig az "1'' keréken. Az $ω_{2}$ -t legkönnyebben a középpontokat összekötő rúdra ülve, az $ω$ szögsebességgel forgó koordinátarendszerben határozhatjuk meg. Ebben a rendszerben az "1'' fogaskerék szögsebessége $ω_{1} - ω$ (a szögsebességek mindig előjelesen értendők), ez olyan sebességgel forgatja a "2''-t, hogy egyenlő idők alatt egyenlő ívdarabok gördüljenek el egymáson, vagyis

\begin{matrix} r_{1} (ω_{1} - ω) | \cdot t = - r_{2} ω_{2} t, \end{matrix}

ebből

\begin{matrix} ω_{2} = - \frac{r_{1}}{r_{2}} (ω_{1} - ω) . \end{matrix}

A pillanatnyi forgástengely azon a ponton fog áthaladni, amely pontnak ‐ az

O_{1}

körüli

ω

és

O_{2}

körüli

ω_{2}

szögsebességű forgás eredőjeként létrejövő ‐ sebessége nulla. Ez a pont csak az

O_{1} O_{2}

egyenesen lehet, mert csak itt párhuzamos az egyes forgásokból adódó sebességek iránya. Tegyük fel, hogy a keresett pont az

O_{1}

-től

x

távolságra, helyezkedik el. Ekkor az

O_{1}

körüli forgásból származó sebessége:

\begin{matrix} v_{1} = x \cdot ω, \end{matrix}

O_{2}

körüli forgásból származó sebessége pedig:

\begin{matrix} v_{2} = [x - (r_{1} + r_{2})] \cdot ω_{2} . \end{matrix}

x

pozitív, ha az

O_{1}

-től az

O_{2}

felé esik. Ezek eredője:

\begin{matrix} v_{1} + v_{2} = x (ω + ω_{2}) - (r_{1} + r_{2}) ω_{2}, \end{matrix}

akkor lesz nulla, ha

\begin{matrix} x = (r_{1} + r_{2}) \frac{r_{1} (ω - ω_{1})}{r_{2} ω + r_{1} (ω - ω_{1})} . \end{matrix}

Szöllősy Péter (Budapest, I. István Gimn., IV. o. t.)

II. megoldás. Bármely időpontban a "2'' kerék középpontjának a sebessége: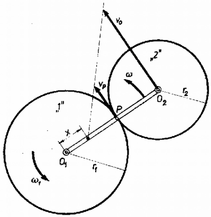

\begin{matrix} v_{0} = (r_{1} + r_{2}) ω . \end{matrix}

Mivel a fogak nem csúszhatnak el egymáson, ezért az érintkezési pontok sebessége egyenlő:

\begin{matrix} v_{p} = r_{1} ω_{1} . \end{matrix}

Ezek ismeretében már meghatározható a pillanatnyi forgástengely. Az nyilvánvaló, hogy ez csak a két középpontot összekötő egyenesen lehet, mivel mindkét említett sebesség merőleges erre, mégpedig olyan pontban, amely körül az adott pillanatban a "2'' kerék mozgása egyetlen forgásként fogható fel, azaz minden pontjának a sebessége úgy irható fel, mint az ettől a ponttól való távolság és az erre a pontra vonatkozó pillanatnyi

Ω

szögsebesség szorzata (1. ábra).

1. ábra

Jelöljük ennek a pontnak az

O_{1}

-től való távolságát

x

-szel. Ekkor az

O_{2}

sebessége így írható fel:

\begin{matrix} v_{0} = (r_{1} + r_{2} - x) Ω = (r_{1} + r_{2}) ω, \end{matrix}

P

ponté pedig:

\begin{matrix} v_{p} = (r_{1} - x) Ω = r_{1} ω_{1} . \end{matrix}

Ezt a két egyenletet megoldva

x

-re és

Ω

-ra azt kapjuk, hogy

\begin{matrix} Ω & = ω + \frac{r_{1}}{r_{2}} (ω - ω_{1}), \\ x & = (r_{1} + r_{2}) \frac{r_{1} (ω - ω_{1})}{r_{2} ω + r_{1} (ω - ω_{1})} . \end{matrix}

Szalai Gábor (Bp., Piarista Gimn., IV. o. t.)

Megjegyzések. 1. A "2'' fogaskerék mozgását mindig származtathatjuk az

ω_{1} = 0

esetből. Ha ugyanis az "1'' fogaskerék helyett egy álló

r'_{1} = x

sugarú fogaskereket veszünk, az

O_{2}

tengelyre pedig egy

r'_{2} = r_{1} + r_{2} - x

sugarú fogaskereket erősítünk a "2'' mellé, akkor a középpontokat összekötő rudat

ω

szögsebességgel forgatva az

r'_{2}

sugarú kerék gördülni fog az

r'_{1}

-n, a vele együtt forgó "2'' kerék pedig ugyanúgy fog mozogni, mint eredetileg.
Ha

x > r_{1} + r_{2}

akkor az

r_{2}

sugarú kör az

r'_{1}

sugarú, kör belsejében fog gördülni (2. ábra).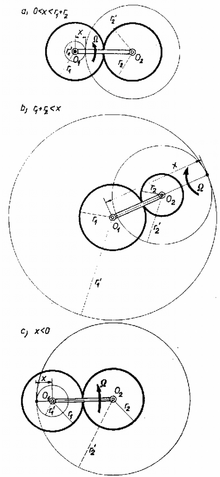

2. ábra

x > 0

, akkor pedig az

r'_{1}

sugarú kör lesz az

r'_{2}

sugarú kör belsejében.

Bajmóczy Ervin (Bp.Fazekas M. Gimn., II. o. t.)

2. A megoldások során csak állapítottuk meg, hogy ha van pillanatnyi forgástengely, akkor az csak az összekötő rúdon az

O_{1}

-tól

x

távolságra lehet. Hogy ez valóban forgástengely, arról mindenki könnyen meggyőződhet azzal, ha felírja a "2'' kerék egy tetszőleges pontjának a sebességét, a mozgást egyetlen forgásnak, ill. két forgás eredőjének tekintve.

3. Sokan azt írták, "a "2'' kerék mozgása az

ω

forgásból és egy

v_{0} = (r_{1} + r_{2}) ω

sebességű haladó mozgásból tevődik őssze.'' Ez óriási tévedés. Ugyanazt a hibát követték el, mint az a megoldó, aki azt írta, hogy "ha

ω_{1} = ω

, akkor az

r_{2}

súgarú kerék nem forog. Elfeledkeztek arról, hogy habár egy testet egy rajta kívül haladó tengely körül forgatunk meg

ω

szögsebességgel, azért annak bármely pontját választva, az egésznek a mozgása úgy fogható fel, mint a körül a bizonyos pont körüli ugyanazzal az

ω

-val való forgás (és persze ehhez járulhat még egy haladó mozgás). Jól látható ez

ω_{1} = ω

esettén a 3. ábrán.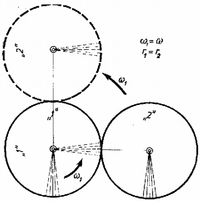

3. ábra

A további félreértések elkerülése érdekében összefoglaljuk, milyen is lehet egy merev test általános mozgása. Csak rövid tényközlésre szorítkozhatunk, a részletesebb bizonyítást lásd Budó Ágoston Mechanika című könyvében. Először is azt kell leszögezni, hogy a szögsebesség vektormennyiség, amelynek az iránya megadja a forgástengely irányát, az abszolút értéke pedig a szögsebesség nagyságát. Az általános esetet egy példán fogjuk szemléltetni. Vegyünk egy merev testet, forgassuk ezt meg a

P_{1}

pontja körül

{\vec{ω}}_{1}

szögsebességgel, és tegyük fel egy

{\vec{v}}_{1}

sebességgel haladó autóra. Haladjon ez az autó egy hatalmas óceánjárón, amely éppen

{\vec{ω}}_{2}

szögsebességgel kanyarodik, miközben a

{\vec{v}}_{2}

sebességű Golf-áramban halad. Mindezen mozgásokhoz hozzáadódik még az, hogy a Föld

{\vec{ω}}_{3}

szögsebességgel forog a saját tengelye körül, és

{\vec{ω}}_{4}

szögsebességgel kering a Nap körül, végül az egyszerűség kedvéért tegyük fel, hogy a Nap

{\vec{v}}_{3}

sebességgel mozog az állócsillagokhoz képest (valójában ez is bizonyos szögsebességgel kering a Tejút centruma körül). Feltehetjük a kérdést, hogy milyen lesz a merev testünk mozgása az állócsillagokhoz viszonyítva. A fizika, vagy inkább a geometria törvényei szerint a testünknek ez a bonyolult mozgása egyetlen forgó és egy haladó mozgás összegére vezethető vissza. Ez úgy értendő, hogy egy tetszőleges pontot felvéve a testen a pillanatnyi mozgás úgy írható fel, hogy a haladó mozgás sebessége egyenlő ennek a kiválasztott pontnak a sebességével, és a test e pont körüli forgásának a szögsebessége pedig egyenlő az összes forgó mozgások szögsebességeinek vektori összegével, azaz a pillanatnyi szögsebesség a jelen esetben:

\begin{matrix} \vec{Ω} = {\vec{ω}}_{1} + {\vec{ω}}_{2} + {\vec{ω}}_{3} + {\vec{ω}}_{4} \end{matrix}

Jól jegyezzük meg tehát, hogy bármelyik pontját is választjuk ki, a test e kiválasztott pont körül mindig ugyanakkora

\vec{Ω}

-val fog forogni, a haladó mozgás pillanatnyi sebessége azonban már függ ennek a referenciapontnak a megválasztásától, ezért nem is adunk meg itt rá semmi képletet.
Láttuk, ha önkényesen választjuk meg a referenciapontot, akkor a mozgás általában két részből tevődik össze: haladó és forgó mozgásból. De ha lemondunk erről az önkényről, és egy olyan pontot; választunk referenciapontnak, amelynek a sebessége nulla ‐

Ω \neq 0

esetén ezt mindig megtehetjük, bár lehet, hogy az ilyen pontok a testen kívül helyezkednek el, de képzeletben a testet meghosszabbíthatjuk akár addig is ‐, akkor csak a forgó mozgás marad.
Külön figyelmet érdemel az

Ω = 0

eset. Ezért vizsgáljuk meg ezt a fogaskerekeink esetén is. A második megoldásban láttuk, hogy a "2'' kerék eredő szögsebessége: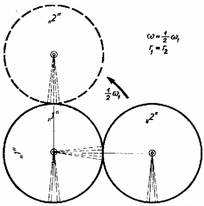

\begin{matrix} Ω = ω + \frac{r_{1}}{r_{2}} (ω - ω_{1}) . \end{matrix}

Vagyis ez akkor fog csak haladó mozgást végezni, ha

\begin{matrix} ω = ω_{1} \frac{r_{1}}{r_{1} + r_{2}} . \end{matrix}

A 4. ábrán látható

r_{1} = r_{2}

esetén, amikor

ω = \frac{1}{2} ω_{1}

, mit is jelent ez a haladó mozgás.

4. ábra

Vagyis nem

ω_{1} = ω

esetén, hanem ekkor hiányzik a forgó mozgás, és bár nincs forgás, a "2'' kerék mégis körbe megy.