Kezdőlap


Feladat:	816. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bálványos Zoltán , Gyimesi Ferenc , Horváthy Péter , Korpássy Péter , Lempert László , Maróti Péter , Spitzer József , Walthier Tamás
Füzet:	1969/december, 226 - 232. oldal		PDF \| MathML
Témakör(ök):	Egyéb merev test síkmozgások, Coulomb-törvény, Feladat
Hivatkozás(ok):	Feladatok: 1969/január: 816. fizika feladat

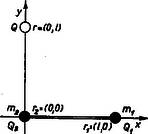
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A feladatban négy objektum szerepel: a $Q_{1}$ töltésű $m_{1}$ tömeg, a $Q_{2}$ töltésű $m_{2}$ tömeg, a rögzített $Q$ töltés és a súlytalan merev szigetelő rúd. A megoldást a Newton-axiómák következetes alkalmazásával kaphatjuk meg. (A hangsúly itt a következetességen, amely sajnos a megoldók többségénél hiányzott.) Vegyük fel az 1.ábrán látható koordináta-rendszert. A $Q_{2}$ töltés az origóba, a $Q_{1}$ az $x$ tengelyre, a $Q$ pedig az $y$ tengelyre essék.

1. ábra

Newton II. axiómája azt mondja, hogy az egyes testek tömegének és gyorsulásának szorzata egyenlő a ráható összes erők eredőjével. Ebben talán a leglényegesebb az összes szó, legalábbis erről feledkeztek meg a legtöbben. Vizsgáljuk meg tehát külön-külön az egyes objektumokra ható összes erőt, majd ezután határozzuk meg ezek eredőjét.
Az

r_{2} = (0,0)

pontbeli

Q_{2}

töltésre ható erők ‐

2 a

ábra ‐ a következők. (A továbbiakban egyszerűség kedvéért figyelmen kívül hagyjuk a tömegek között fellépő, az elektromos erőkhöz képest elenyésző nagyságú gravitációs erőket, nem ez az erő hiányzott az ,,összes'' erők közül. A 816. feladat megoldásánál a vektorok derékszögű komponenseit zárójelben tüntetjük fel.)
1. Az

r = (0, l)

-beli

Q

töltésből származó Coulomb-erő (lásd a megjegyzést):

\begin{matrix} F_{1}^{(2)} = k \frac{Q Q_{2}}{{| r_{2}-r |}^{2}} \cdot \frac{r_{2} - r}{| r_{2} - r |} = (0, - k \frac{Q Q_{2}}{l^{2}}) \end{matrix}

2. Az

r_{1} = (l,0)

-beli

Q_{1}

töltésből pedig

\begin{matrix} F_{2}^{(2)} = k \frac{Q_{1} Q_{2}}{{| r_{2}-r |}^{2}} \cdot \frac{r_{2} - r_{1}}{| r_{2} - r_{1} |} = (- k \frac{Q_{1} Q_{2}}{l^{2}},0) \end{matrix}

Coulomb erő hat.
3. A

Q_{1}

-t és a

Q_{2}

-t összekötő rúd a közvetlen mechanikai csatlakozás révén (ez az, amiről oly sokan megfeledkeztek)

\begin{matrix} F_{3}^{(2)} = (K_{2},0) \end{matrix}

erővel hat a

Q_{2}

töltésre, amely a rúd vékony és merev volta miatt csak

x

irányú lehet. Azt azonban még egyelőre nem tudjuk, hogy ez a

K_{2}

mekkora.

2. ábra

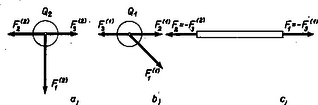
Hasonló módon a

Q_{1}

töltésre ható erők (

2 b

ábra):
1. A Coulomb erő a

Q

töltésből

\begin{matrix} F_{1}^{(1)} = k \frac{Q Q_{1}}{| {r_{1}-r |}^{2}} \cdot \frac{r_{1} - r}{| r_{1} - r |} = k \frac{Q Q_{1}}{{2 l}^{2}} \cdot (\frac{l}{\sqrt[]{2} l}, \frac{- 1}{\sqrt[]{2} l}) = (k \frac{Q Q_{1}}{\sqrt[]{8} l^{2}}, - k \frac{Q Q_{1}}{\sqrt[]{8} l^{2}}) . \end{matrix}

2. A

Q_{2}

-ből származó Coulomb erő:

\begin{matrix} F_{2}^{(1)}=-F_{2}^{(2)} = (+ k \frac{Q_{1} Q_{2}}{l^{2}},0) . \end{matrix}

3. Az összekötő rúd nyilvánvalóan erre is csak

x

irányú erővel hat:

\begin{matrix} F_{3}^{(1)} = (K_{1},0) . \end{matrix}

Mivel a

Q

töltés rögzítve van, így akármekkora erő is hat reá, nem jöhet létre gyorsulás (,,végtelen'' a tömege), ezért nem érdekesek a ráható erők. Annál érdekesebbek viszont az összekötő rúdra ható erők (

2 c

ábra). Mivel a rúd

F_{3}^{(1)}

erővel hat a

Q_{1}

töltésre, ezért a rúdra a III. axióma értelmében

{F_{1}=-F}_{3}^{(1)} = (- K_{1},0)

erő hat, ugyanígy hat persze a rúdra az

F_{3}^{(2)}

erő ellenereje is, az

{F_{2}=-F}_{3}^{(2)} = (- K_{2},0)

erő. Most alkalmazzuk Newton II. axiómáját először az összekötő rúdra. Mivel ennek tömege nulla, ezért az erők összege:

\begin{matrix} m a = F_{1}+F_{2} = 0, \end{matrix}

amely komponensekre kiírva azt jelenti, hogy

\begin{matrix} - K_{1} - K_{2} & = 0, & (1) \\ 0 + 0 & = 0. \end{matrix}

Vagyis

K_{1} = - K_{2}

amely felére csökkenti ugyan az ismeretlenek számát, de még mindig ismeretlen marad a rúdban ébredő erő. Ennek az az oka, hogy ezt a

K_{1}

erőt, az ún. kényszererőt ‐ amely azért hat a két tömeg között, mert azok mozgása és így a gyorsulása nem lehet tetszőleges, ugyanis a rúd merevsége miatt a két tömeg távolsága nem változhat ‐ meghatározó feltételt még eddig nem vettük figyelembe. Ez a geometriai feltétel matematikailag azt jelenti, hogy

\begin{matrix} ∣ r_{1} (t) - r_{2} (t) ∣^{2} = l^{2} . \end{matrix}

Ezt az összefüggést felhasználva próbáljunk valamilyen kapcsolatot keresni a gyorsulások között. Ha az

m_{1}

, ill. az

m_{2}

tömeg gyorsulása a kezdetben

a_{1}

, ill.

a_{2}

, és

a

kezdősebességük nulla, akkor egy kis

Δ t

idő alatt az elmozdulásuk

\begin{matrix} (\frac{a_{1 x}}{2} Δ t^{2}, \frac{a_{1 y}}{2} Δ t^{2}) = Δ r_{1}, illetve (\frac{a_{2 x}}{2} Δ t^{2}, \frac{a_{2 y}}{2} Δ t^{2}) = Δ r_{2}, vagyis \\ r_{1} (t = Δ t) = r_{1} (0) + Δ r_{1} = (1 + \frac{a_{1 x}}{2} Δ t^{2}, + \frac{a_{1 y}}{2} Δ t^{2}), \\ r_{2} (t = Δ t) = r_{2} (0) + Δ r_{2} = (\frac{a_{2 x}}{2} Δ t^{2}, + \frac{a_{2 y}}{2} Δ t^{2}), \end{matrix}

Ezt behelyettesítve a geometriai feltételbe:

\begin{matrix} l^{2} = {(l + \frac{a_{1 x}}{2} Δ t^{2} - \frac{a_{2 x}}{2} Δ t^{2})}^{2} + {(\frac{1}{2} a_{1 y} Δ t^{2} - \frac{1}{2} a_{2 y} Δ t^{2})}^{2} \end{matrix}

Ebből

\begin{matrix} - l (a_{1 x} - a_{2 y}) Δ t^{2} = \frac{1}{4} [{(a_{1 x} - a_{2 x})}^{2} + {(a_{1 y} - a_{2 y})}^{2}] Δ t^{4} . \end{matrix}

Δ t^{2}

-tel egyszerűsítve:

\begin{matrix} - l (a_{1 x} - a_{2 x}) = \frac{1}{4} [{(a_{1 x} - a_{2 x})}^{2} + {(a_{1 y} - a_{2 y})}^{2}] Δ t^{2} . \end{matrix}

Δ t

nagyon kicsi, akkor a jobb oldalon gyakorlatilag nulla áll, ezért ebből az következik, hogy

\begin{matrix} a_{1 x} = a_{2 x} . \end{matrix}

(2)

Nem szabad azonban elfeledkezni arról, hogy ez csak a kezdőpillanatra igaz! De ez számunkra éppen elég.
Most írjuk fel az

m_{1}

és az

m_{2}

tömegekre a II. axiómát:

\begin{matrix} m_{1} a_{1} = F_{1}^{(1)} + F_{2}^{(1)} + F_{3}^{(1)} és m_{2} a_{2} = F_{1}^{(2)} + F_{2}^{(2)} + F_{3}^{(2)} . \end{matrix}

Az erőket behelyettesítve és az egyenleteket komponensenként kiírva:

\begin{matrix} m_{1} a_{1 x} & = k \frac{Q Q_{1}}{\sqrt[]{8} l^{2}} + k \frac{Q_{1} Q_{2}}{l^{2}} + K_{1}, & (3) \\ m_{1} a_{1 y} & = - k \frac{Q Q_{1}}{\sqrt[]{8} l^{2}} + 0 + 0, & (4) \\ m_{2} a_{2 x} & = 0 - k \frac{Q_{1} Q_{2}}{l^{2}} + (- K_{1}) = m_{2} a_{1 x}, & (5) \\ m_{2} a_{2 y} & = - k \frac{Q Q_{2}}{l^{2}} + 0 + 0. & (6) \end{matrix}

Az (5) egyenlet felírásánál felhasználtuk az (1) és a (2) egyenleteket. Ebben a négy egyenletben négy ismeretlen van:

a_{1 x}

a_{1 y}

a_{2 y}

és

K_{1}

. A (3)

m_{2}

-szeresét és az (5)

m_{1}

-szeresét véve egyenletet kapunk

K_{1}

-re:

\begin{matrix} m_{2} k \frac{Q_{1}}{l^{2}} (\frac{Q}{\sqrt[]{8}} + Q_{2}) + m_{2} K_{1} = - m_{1} k \frac{Q_{1} Q_{2}}{l^{2}} - m_{1} K_{1} . \end{matrix}

Ebből:

\begin{matrix} K_{1} = - k \frac{Q_{1}}{l^{2}} [\frac{Q}{\sqrt[]{8}} \frac{m_{2}}{m_{1} + m_{2}} + Q_{2}] . \end{matrix}

Ekkora erő hat tehát a rúdban. Ezt visszahelyettesítve sorra kifejezhetjük az egyes gyorsulásokat is:

\begin{matrix} a_{1 x} = \frac{k}{m_{1} + m_{2}} \frac{Q Q_{1}}{\sqrt[]{8} l^{2}}, a_{1 y} = - \frac{k}{m_{1}} \frac{Q Q_{1}}{\sqrt[]{8} l^{2}}, \\ a_{2 x} = \frac{k}{m_{1} + m_{2}} \frac{Q Q_{1}}{\sqrt[]{8} l^{2}}, a_{2 y} = \frac{k}{m_{2}} \frac{Q Q_{2}}{\sqrt[]{8} l^{2}}, \end{matrix}

Maróti Péter (Szeged, Ságvári E. Gimn., IV. o. t.)

II. megoldás. Csak az tudja igazán értékelni a következő megoldást, aki végigolvasta az előző, közvetlenül a Newton-axiómákon alapuló megoldást. Bár végső soron ez az egyszerű megoldás is ezeken alapul, csak éppen a feladathoz jobban illő alakjukat használja fel. A Newton-axiómák egyik közvetlen következménye a tömegközéppont mozgásának tétele, amely szerint egy pontrendszer súlypontja úgy mozog, mintha az egész tömeg abba lenne koncentrálva, és arra hatna az összes külső erő. Egyrészt ezt fogjuk felhasználni, másrészt pedig azt, hogy egy merev test szöggyorsulása egyenlő a forgatónyomaték és a tehetetlenségi nyomaték hányadosával. (Ez az egyenlet azonos Newton II. axiómájával, csak éppen azt ügyes, a probléma lényegét ‐ a merevséget‐ jól megragadó paraméterekkel írja fel. Az egyes tömegeket a tehetetlenségi nyomatékba, az egyes erőket az eredő forgatónyomatékba, a sok-sok gyorsulást pedig a szöggyorsulásba sűríti. Így elkerülhetővé válik a kínos geometriai feltételek állandó figyelembe vétele.)
A tömegek gyorsulása két részből tevődik össze: a súlypont gyorsulása plusz. a súlypont körüli szöggyorsulásból eredő gyorsulás. Módszerünk előnye, hogy ez a kettő egymástól függetlenül meghatározható.

3. ábra

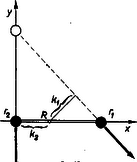
Jelen esetben a pontrendszert a rúd két végén levő tömegek alkotják. A tömegközéppont koordinátája (3. ábra):

\begin{matrix} R = \frac{m_{1} r_{1} + m_{2} r_{2}}{m_{1} + m_{2}} . \end{matrix}

Az ebbe képzelt össztömeg:

\begin{matrix} M = m_{1} + m_{2} . \end{matrix}

A külső erők csak a

Q

-ból származó Coulomb-erők (az előző jelöléseket alkalmazva):

\begin{matrix} F=F_{1}^{(1)}+F_{1}^{(2)} = (k \frac{Q Q_{1}}{\sqrt[]{8} l^{2}}, - k \frac{Q}{l^{2}} (\frac{Q_{1}}{\sqrt[]{8}} + Q_{2})) . \end{matrix}

Tehát a tömegközéppont gyorsulása:

\begin{matrix} a_{x} = \frac{F_{x}}{M} = \frac{k}{m_{1} + m_{2}} \cdot \frac{Q Q_{1}}{\sqrt[]{8} l^{2}}, a_{y} = \frac{F_{y}}{M} = - \frac{k}{m_{1} + m_{2}} \cdot \frac{Q}{l^{2}} (\frac{Q}{\sqrt[]{8}} + Q_{2}) . \end{matrix}

A tömegközéppontra vonatkoztatott tehetetlenségi nyomaték:

\begin{matrix} I = m_{1} {(r_{1}-R)}^{2} + m_{2} {(r_{2}-R)}^{2} = \frac{m_{1} m_{2}}{m_{1} + m_{2}} l^{2} . \end{matrix}

Az egyes külső erők erőkarja (lásd a 3. ábrát):

\begin{matrix} k_{1} = \sqrt[]{2} | r_{1}-R | és k_{2} = | r_{2}-R | . \end{matrix}

Így az eredő forgatónyomaték:

\begin{matrix} M = - k_{1} | F_{1}^{(1)} | + k_{2} | F_{1}^{(2)} | = - \frac{m_{2}}{m_{1} + m_{2}} l \cdot k \frac{Q Q_{1}}{\sqrt[]{8} l^{2}} + \frac{m_{1}}{m_{1} + m_{2}} l \cdot k \frac{Q Q_{2}}{l^{2}} . \end{matrix}

Ebből a szöggyorsulás:

\begin{matrix} β = \frac{M}{I} = k \frac{Q}{l^{2}} [- \frac{1}{m_{1}} \cdot \frac{Q_{1}}{\sqrt[]{8} l} + \frac{1}{m_{2}} \cdot \frac{Q_{2}}{l}] . \end{matrix}

A tömegeknek a forgásból származó gyorsulása kezdetben csak

y

irányú, mert a súlypont körül történik a forgás. Ezért az

x

-irányú gyorsulásuk egyenlő, nagysága pedig megegyezik a tömegközéppont

x

-irányú gyorsulásával, tehát

\begin{matrix} a_{1 x} = a_{2 x} = \frac{k}{m_{1} + m_{2}} \frac{Q Q_{1}}{\sqrt[]{8} l^{2}} . \end{matrix}

m_{1}

tömeg forgásból származó

y

-irányú gyorsulása:

\begin{matrix} a_{1 y}^{forg} = | r_{1}-R | β = \frac{k}{m_{1} + m_{2}} \frac{Q}{l^{2}} [- \frac{m_{2}}{m_{1}} \cdot \frac{Q_{1}}{\sqrt[]{8}} + Q_{2}], \end{matrix}

m_{2}

tömegé pedig

\begin{matrix} a_{2 y}^{forg} = - | r_{2}-R | β = \frac{k}{m_{1} + m_{2}} \frac{Q}{l^{2}} [- \frac{m_{1}}{m_{2}} Q_{2} + \frac{Q_{1}}{\sqrt[]{8}}] . \end{matrix}

A haladó és forgó mozgás

y

-irányú eredője:

\begin{matrix} a_{1 y} = a_{y} + a_{1 y}^{forg} = - \frac{k}{m_{1}} \cdot \frac{Q Q_{1}}{\sqrt[]{8} l^{2}}, \\ a_{2 y} = a_{y} + a_{2 y}^{forg} = - \frac{k}{m_{2}} \cdot \frac{Q Q_{2}}{l^{2}} . \end{matrix}

Ennek a megoldásnak előnye és ugyanakkor hátránya, hogy nem jelenik meg benne a rúdban ébredő erő. Persze a gyorsulások ismeretében könnyen meghatározhatjuk ezt is. Ez azonban az előző megoldáshoz képest nem jelentene semmi újat, hiszen újra csak a (3) vagy az (5) egyenletből kellene

K_{1}

-et kifejezni.

Horváthy Péter (Budapest., Fazekas M. Gimn., III. o. t.)

III. megoldás. Az

x

-irányú gyorsulás egyszerűbben is meghatározható, ha abból indulunk ki, hogy az egész rúd

x

-irányú elmozdulása csak a

Q

és a

Q_{1}

közötti Coulomb-erőnek a rúd irányába eső komponensének a hatására következik be. Vagyis

\begin{matrix} a_{1 x} = a_{2 x} = k \frac{Q Q_{1}}{2 l^{2}} \cdot \frac{1}{\sqrt[]{2}} \cdot \frac{1}{m_{1} + m_{2}} . \end{matrix}

A rúdban ébredő erőnek eleve csak

x

-komponense lehet, ez két részből tevődik össze: a

Q_{1}

és a

Q_{2}

közötti Coulomb-erőt ellensúlyozó erő, és az

m_{2}

tömeg

a_{2 x}

gyorsulását létrehozó

m_{2} a_{2 x}

erő. Tehát a rúdban ébredő erő:

\begin{matrix} K = k \frac{Q_{1} Q_{2}}{l^{2}} + \frac{m_{2}}{m_{1} + m_{2}} \cdot k \frac{Q Q_{1}}{2 l^{2}} \cdot \frac{1}{\sqrt[]{2}} . \end{matrix}

Walthier Tamás (Bp., Piarista Gimn., III. o. t. )

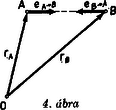
Megjegyzés. Foglalkozzunk egy kicsit részletesebben a Coulomb-törvénnyel, ill. a hozzá nagyon hasonló Newton-féle gravitációs törvénnyel. Általában csak azt szokták mondani, hogy a két tömeg (töltés) között fellépő erő egyenlő a két tömeg (töltés) szorzatának és a köztük levő távolság négyzetének a hányadosával, amelyet meg kell szorozni egy megfelelő állandóval. (Az állandó elsősorban az egységek megválasztásával van kapcsolatban.) Ez azonban az erőnek csak a nagysága. Az erő viszont vektor mennyiség, ezért meg kell adni az irányát is. Szóban ezt úgy szokták elintézni, hogy az erő centrális, azaz a két tömeget összekötő egyenes mentén hat, előjele pedig olyan, hogy a két tömeg vonzza egymást, két töltés esetén az egyneműek taszítják, a különneműek vonzzák egymást. Mi azonban egy általános képletet szeretnénk, amelyben nem kell külön-külön megvizsgálni az ilyen speciális eseteket. Ehhez pedig nem kell mást tenni, mint megadni egy olyan egységnyi hosszúságú vektort, amelynek az iránya megegyezik az erő irányával.

Ha a két objektumot

A

-val és

B

-vel jelöljük, és ezek az

r_{A}

ill.

r_{B}

helyvektorral jelzett pontokban helyezkednek el (4. ábra), akkor az

A

-ból a

B

-be mutató egységvektor:

\begin{matrix} e_{A \to B}=\frac{r_{B} - r_{A}}{| r_{B} - r_{A} |} . \end{matrix}

B

-ből az

A

-ba mutató egységvektor pedig:

\begin{matrix} e_{B \to A}=-e_{A \to B}\frac{r_{A} - r_{B}}{| r_{A} - r_{B}}|, \end{matrix}

ahol

| r_{B}-r_{A}|=|r_{A}-r_{B}|

r_{A}-r_{B}

vektor hossza, azaz az

A

és

B

pontok távolsága. Ebből a gravitációs erő általános vektoralakja, ha az

A

pontban

m_{A}

, a

B

pontban

m_{B}

tömeget helyezünk el: a) Az

m_{A}

tömegre ható gravitációs erő:

\begin{matrix} F_{A} = f \frac{m_{A} \cdot m_{B}}{{| r_{A}-r_{B} |}^{2}} \cdot e_{A \to B} = f \frac{m_{A} \cdot m_{B}}{{| r_{A}-r_{B} |}^{2}} \cdot \frac{r_{B} - r_{A}}{| r_{A} - r_{B} |} . \end{matrix}

b) Az

m_{B}

tömegre ható gravitációs erő:

\begin{matrix} F_{B} = f \frac{m_{A} \cdot m_{B}}{{| r_{A}-r_{B} |}^{2}} \cdot e_{B \to A} = f \frac{m_{A} \cdot m_{B}}{{| r_{A}-r_{B} |}^{2}} \cdot \frac{r_{A} - r_{B}}{| r_{A} - r_{B} |} . \end{matrix}

A Coulomb erő általános alakja csak annyiban tér el ettől, hogy figyelembe kell venni a töltések előjelét is.
a) A

Q_{A}

(előjelesen vett) töltésre ható Coulomb erő:

\begin{matrix} F_{A} = - k \frac{Q_{A} Q_{B}}{{| r_{A}-r_{B} |}^{2}} \cdot e_{A \to B} = k \frac{Q_{A} Q_{B}}{{| r_{A}-r_{B} |}^{2}} \cdot \frac{r_{A} - r_{B}}{| r_{A} - r_{B} |} . \end{matrix}

ahol a mínusz előjel azért szükséges, mert ha a tőkések előjele azonos, akkor nyilvánvalóan az iránnyal ellentétes irányú taszító erő lép fel.
b) A

Q_{B}

töltésre így

\begin{matrix} F_{B} = - k \frac{Q_{B} Q_{A}}{{| r_{B}-r_{A} |}^{2}} \cdot e_{B \to A} = k \frac{Q_{B} Q_{A}}{{| r_{B}-r_{A} |}^{2}} \cdot \frac{r_{B} - r_{A}}{| r_{B} - r_{A} |} . \end{matrix}

Coulomb erő hat.