Kezdőlap


Feladat:	807. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Korpássy Péter , Sailer Kornél , Váradi József
Füzet:	1969/október, 89 - 90. oldal		PDF \| MathML
Témakör(ök):	Lencserendszerek, Feladat
Hivatkozás(ok):	Feladatok: 1968/december: 807. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Lencserendszerünket úgy helyezzük el, hogy az első, $f_{1}$ gyújtótávolságú lencse a tárgytól $x$ távolságnyira legyen (1. ábra).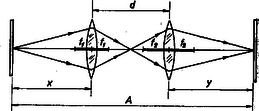

1. ábra

A tárgyról az első lencse a leképezési törvény szerint

x f_{1} / (x - f_{1})

távolságban ad éles képet, amely a második lencsétől

d - x f_{1} / (x - f_{1})

távolságban van. Ismét a lencsetörvénnyel számolva a keletkezett képről, mint tárgyról a második lencse

y

távolságban ad képet:

\begin{matrix} y = \frac{f_{2} (d - f_{1}) x - f_{1} f_{2} d}{(d - f_{1} - f_{2}) x + f_{1} (f_{2} - d)} . \end{matrix}

A tárgy és kép egymástól mért távolsága:

A = x + d + y

y

kiszámított értékét felhasználva és a kifejezést rendezve:

\begin{matrix} A = d + \frac{(d - f_{1} - f_{2}) x^{2} + (f_{2} - f_{1}) d x - f_{1} f_{2} d}{(d - f_{1} - f_{2}) x + f_{1} (f_{2} - d)} . \end{matrix}

Az a feltétel, hogy

A

, a tárgy és kép távolsága a lencserendszer minden helyzeténél ugyanaz legyen, akkor valósul meg, ha

A

kifejezése független

x

-től. Ebből következik, hogy

x

és

x^{2}

együtthatóinak

0

-nak kell lenniök, így egyrészt

\begin{matrix} f_{2} - f_{1} = 0. \end{matrix}

Tehát a megkívánt feltétel akkor teljesül, ha

f_{2} = f_{1} = f

, vagyis a lencsék gyújtótávolsága egyenlő. Továbbá kell, hogy

\begin{matrix} d - f - f = 0 legyen, \end{matrix}

tehát

d = 2 f

, a lencsék távolsága a gyújtótávolság kétszerese. A tárgy és kép távolsága:

\begin{matrix} A = d + \frac{- f^{2} d}{- f^{2}} = d + d = 2 d = 4 f . \end{matrix}

Az első lencse nagyítása

\frac{x f}{x - f} : x = \frac{f}{x - f}

, a második lencse nagyítása

y : d - \frac{x f}{x - f} = - \frac{x - f}{f}

. A teljes nagyítás a két lencse nagyításának szorzata:

\begin{matrix} \frac{f}{x - f} \cdot \frac{x - f}{- f} = - 1. \end{matrix}

Tehát a lencserendszer elhelyezésétől függetlenül fordított, eredeti nagyságú képet ad.

Sailer Kornél (Ózd, József A. Gimn. III. o. t.)

1. Megjegyzés. A sugármenet egy példája (2. ábra) is mutatja, hogy minden esetben vagy a tárgy, vagy a kép képzetes.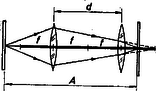

2. ábra

Egyébként a lencserendszer teleszkópikus, vagyis a lencserendszerre eső párhuzamos sugárnyaláb azt párhuzamosan hagyja el.

Korpássy Péter (Budapest, Eötvös J. Gimn. IV. o. t.)

2. Megjegyzés. Az is lehetséges, hogy a lencserendszer az

A

távolságon kívül van (3. ábra).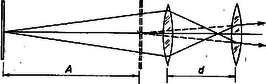

3. ábra

Váradi József (Budapest, Ságvári E. Gimn. IV. o. t.)