Feladat:	799. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Kocsis Ferenc ,  László István ,  Maróti Péter ,  Sághy András ,  Tél Tamás
Füzet:	1969/november, 173 - 176. oldal		PDF  |  MathML
Témakör(ök):	Egyéb váltóáramú áramkörök, Kirchhoff I. törvénye (csomóponti törvény), Kirchhoff II. törvénye (huroktörvény), Feladat
Hivatkozás(ok):	Feladatok: 1968/november: 799. fizika feladat

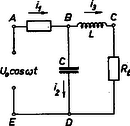
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   a)   b)   c) (Gaál István cikkében szereplő jelöléseket alkalmazzuk, I. K. M. L. 1968. évi 8‐9. szám 165. o.) a) kapcsolás. Kirchhoff I. törvényét a $B$ csomópontra, II. törvényét pedig az $ABDE$ és a $BCD$ körökre felírva három egyenletet kapunk: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle i_1\left(t\right)}& {\displaystyle =i_2\left(t\right)+i_3\left(t\right)\mathrm{,}}\hfill & \text{(1)}\\ \hfill {\displaystyle R{i}_1\left(t\right)}& {\displaystyle +\frac{1}{C}q\left(t\right)=U_0\text{cos}\omega t\mathrm{,}}\hfill & \text{(2)}\\ \hfill {\displaystyle Li{\text{'}}_3\left(t\right)}& {\displaystyle +R_t{i}_3\left(t\right)-\frac{1}{C}q\left(t\right)=0;}\hfill & \text{(3)}\end{array}}$ ahol $q\left(t\right)$ a kondenzátor pillanatnyi töltése: $\begin{array}{c}{\displaystyle i_2\left(t\right)=q\text{'}\left(t\right)\mathrm{.}}\end{array}$ (4) Ez a négyismeretlenes egyenletrendszer megoldható. Nekünk nyilvánvalóan csak $i_3\left(t\right)$-re van szükségünk, ezért a többi változót megpróbáljuk algebrai módszerekkel kiejteni. A (2) és (3) egyenletekben vegyük a bennük szereplő mennyiségek változásának a sebességét, (4) felhasználásával: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle Ri{\text{'}}_1\left(t\right)+\frac{1}{C}{i}_2\left(t\right)}& {\displaystyle =-U_0\omega \text{sin}\omega t\mathrm{,}}\hfill & \text{(<mn>5</mn>)}\\ \hfill {\displaystyle Li\text{'}{\text{'}}_3\left(t\right)+R_{t}i{\text{'}}_3\left(t\right)}& {\displaystyle -\frac{1}{C}{i}_2\left(t\right)=0.}\hfill & \text{(<mn>6</mn>)}\end{array}}$ Kifejezve $i_2\left(t\right)$-t (6)-ból és $i_1\left(t\right)$-t (1)-ből, majd az (5)-be helyettesítve olyan egyenletet kapunk, melyben csak az $i_3\left(t\right)$ függvény az ismeretlen: $\begin{array}{c}{\displaystyle RLCi\text{'}\text{'}{\text{'}}_3\left(t\right)+\left(L+R{R}_{t}C\right)i\text{'}{\text{'}}_3+\left(R+R_t\right)i{\text{'}}_3+U_0\omega \text{sin}\omega t=0.}\end{array}$ (7) Keressük az $i_3\left(t\right)$ ismeretlen függvényt $\begin{array}{c}{\displaystyle i_3\left(t\right)=I\text{sin}\left(\omega t+\phi \right)}\end{array}$ (8) alakban. Az idézett cikk alapján ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle i{\text{'}}_3\left(t\right)}& {\displaystyle =I\omega \text{cos}\left(\omega t+\phi \right)\mathrm{,}}\hfill & \text{(<mn>9</mn>)}\\ \hfill {\displaystyle i\text{'}{\text{'}}_3\left(t\right)}& {\displaystyle =-I{\omega }^2\text{sin}\left(\omega t+\phi \right)\mathrm{,}}\hfill & \text{(<mn>10</mn>)}\\ \hfill {\displaystyle i\text{'}\text{'}{\text{'}}_3\left(t\right)}& {\displaystyle =-I{\omega }^3\text{cos}\left(\omega t+\phi \right)\mathrm{.}}\hfill & \text{(<mn>11</mn>)}\end{array}}$ (7)-be helyettesítve, a $\text{sin}\omega t$ és a $\text{cos}\omega t$ együtthatói el kell, hogy tünjenek: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle \left(R+R_t-{\omega }^{2}RLC\right)\text{sin}\phi +\omega \left(L+R{R}_{t}C\right)\text{cos}\phi }& {\displaystyle =U_0/I\mathrm{,}}\hfill & \text{(<mn>12</mn>)}\\ \hfill {\displaystyle \left(R+R_t-{\omega }^{2}RLC\right)\text{cos}\phi -\omega \left(L+R{R}_{t}C\right)\text{sin}\phi }& {\displaystyle =0.}\hfill & \text{(<mn>13</mn>)}\end{array}}$ Az áram amplitúdójának értékét a két egyenlet négyzetösszegéből kifejezhetjük, és így az $R_t$ ellenálláson megjelenő feszültség amplitúdója $\begin{array}{c}{\displaystyle U=I\cdot R_t=\frac{U_0{R}_t}{\sqrt[]{{\left(R+R_t-{\omega }^{2}RLC\right)}^2+{\omega }^2{\left(L+R{R}_{t}C\right)}^2}}\mathrm{,}}\end{array}$ (14) vagyis $\begin{array}{c}{\displaystyle U=\frac{\alpha }{\sqrt[]{{\gamma }_1{\omega }^4+{\gamma }_2{\omega }^2+{\gamma }_3}}}\end{array}$ (15) alakú a feszültség, ahol az $\alpha$ és a $\gamma$-k konstansok. A (13) egyenletből $\begin{array}{c}{\displaystyle \text{tg }\phi =\frac{R+R_t-{\omega }^{2}RLC}{\omega \left(L+R{R}_{t}C\right)}\mathrm{,}}\end{array}$ (16) így az $R_t$ ellenálláson megjelenő feszültség $\begin{array}{c}{\displaystyle u_t\left(t\right)=U\text{sin}\left(\omega t+\phi \right)\mathrm{,}}\end{array}$ (17) ahol $U$ és $\phi$ a (14) és (16) egyenletekben adottak. 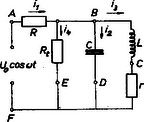b) kapcsolás. Kirchhoff I. törvényét a $B$ csomópontra, II. törvényét pedig az $ABEF$, a $BCE$ és a $BDE$ körökre felírva négy egyenletet kapunk: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle i_1\left(t\right)}& {\displaystyle =i_2\left(t\right)+i_3\left(t\right)+i_4\left(t\right)\mathrm{,}}\hfill & \text{(<mn>18</mn>)}\\ \hfill {\displaystyle R{i}_1\left(t\right)}& {\displaystyle +R_t{i}_4\left(t\right)=U_0\text{cos}\omega t\mathrm{,}}\hfill & \text{(<mn>19</mn>)}\\ \hfill {\displaystyle Li{\text{'}}_3\left(t\right)}& {\displaystyle +r{i}_3\left(t\right)-R_t{i}_4\left(t\right)=\mathrm{0,}}\hfill & \text{(<mn>20</mn>)}\\ \hfill {\displaystyle \frac{1}{C}}& {\displaystyle q\left(t\right)-R_t{i}_4\left(t\right)=0;}\hfill & \text{(<mn>21</mn>)}\end{array}}$ valamint tudjuk, hogy $\begin{array}{c}{\displaystyle i_2\left(t\right)=q\text{'}\left(t\right)\mathrm{.}}\end{array}$ (22) Az a) kapcsolásnál végzett számításokhoz hasonlóan ez az egyenletrendszer algebrai módszerekkel a következőre redukálható: ${\displaystyle \begin{array}{c}\hfill {\displaystyle LR{R}_{t}Ci\text{'}{\text{'}}_4\left(t\right)+\left(LR+L{R}_t+rR{R}_{t}C\right)i{\text{'}}_4\left(t\right)+}\hfill \\ \hfill {\displaystyle +\left(rR+R{R}_t+r{R}_t\right)i_4\left(t\right)+U_0\left(\omega L\text{sin}\omega t-r\text{cos}\omega t\right)=0.}\hfill & \text{(<mn>23</mn>)}\end{array}}$ Az $i_4\left(t\right)$ megoldásfüggvényt keressük a (8)‐(9)‐(10) képleteknek megfelelő alakban: (24) (23)-ba helyettesítve $\text{sin}\omega t$ és $\text{cos}\omega t$ együtthatója el kell, hogy tűnjék: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }& {\displaystyle \left(rR+R{R}_t+r{R}_t-{\omega }^{2}LR{R}_{t}C\right)\text{cos}\phi -\omega \left(LR+L{R}_t+rR{R}_{t}C\right)\text{sin}\phi =-\frac{\omega L}{I}{U}_0\mathrm{,}}\hfill & \text{(<mn>25</mn>)}\\ \hfill {\displaystyle }& {\displaystyle \left(rR+R{R}_t+r{R}_t-{\omega }^{2}LR{R}_{t}C\right)\text{sin}\phi +\omega \left(LR+L{R}_t+rR{R}_{t}C\right)\text{cos}\phi =\frac{r}{I}{U}_0\mathrm{.}}\hfill & \text{(<mn>26</mn>)}\end{array}}$ A két egyenlet négyzetösszegéből a keresett feszültség amplitúdója: $\begin{array}{c}{\displaystyle U=I{R}_t=U_0{R}_t\sqrt[]{\frac{r^2+{\omega }^2{L}^2}{{\left(rR+R{R}_t+r{R}_t-{\omega }^{2}LR{R}_{t}C\right)}^2+{\omega }^2{\left(LR+L{R}_t+rR{R}_{t}C\right)}^2}}\mathrm{.}}\end{array}$ (27) Azaz (15)-höz hasonlóan $\begin{array}{c}{\displaystyle U=\sqrt[]{\frac{{\alpha }_1{\omega }^2+{\alpha }_2}{{\gamma }_1{\omega }^4+{\gamma }_2{\omega }^2+{\gamma }_3}}\mathrm{.}}\end{array}$ (28) (25)-öt $r$-rel, (26)-ot $\omega L$-lel beszorozva és összeadva megkapjuk a fázisszöget: $\begin{array}{c}{\displaystyle \text{tg }\phi =\frac{\left(R+R_t\right)\left(r^2+{\omega }^2{L}^2\right)+rR{R}_t}{\omega R{R}_t\left[C\left(r^2+{\omega }^2{L}^2\right)-L\right]}\mathrm{,}}\end{array}$ (29) így az $R_t$ ellenálláson megjelenő feszültség (30) ahol $U$ és $\phi$ a (27) és (29) egyenletekben adottak. 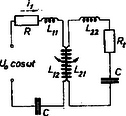c) kapcsolás. (Az ábra elvi kapcsolási rajz. Valójában az $L_{11}$, illetve $L_{22}$ önindukciós együtthatók nem függetlenek és nem választhatóak külön az $L_{12}$, illetve $L_{21}$ kölcsönös indukciós együtthatóktól. Ugyanez volt a helyzet a b) esetben az $L$ önindukciós együtthatójú tekercs $r$ veszteségi ellenállásával is.)   Kirchhoff II. törvényét mind a két körre külön-külön felírjuk ($q_1\left(t\right)$ a bal oldali, $q_2\left(t\right)$ a jobb oldali kondenzátor töltése): ${\displaystyle \begin{array}{cc}\hfill {\displaystyle R{i}_1\left(t\right)+L_{11}i{\text{'}}_1\left(t\right)+L_{12}i{\text{'}}_2\left(t\right)+\frac{1}{C}{q}_1\left(t\right)=U_0\text{cos}\omega t\mathrm{,}}\hfill & \text{(<mn>31</mn>)}\\ \hfill {\displaystyle R_t{i}_2\left(t\right)+L_{22}i{\text{'}}_2\left(t\right)+L_{21}i{\text{'}}_1\left(t\right)+\frac{1}{C}{q}_2\left(t\right)=\mathrm{0,}}\hfill & \text{(<mn>32</mn>)}\end{array}}$ valamint ${\displaystyle \begin{array}{cc}\hfill {\displaystyle i_1\left(t\right)=q{\text{'}}_1\left(t\right)\mathrm{,}}\hfill & \text{(<mn>33</mn>)}\\ \hfill {\displaystyle i_2\left(t\right)=q{\text{'}}_2\left(t\right)}\hfill & \text{(<mn>34</mn>)}\end{array}}$ és $\begin{array}{c}{\displaystyle L_{12}=L_{21}\mathrm{.}}\end{array}$ (35) A töltéseket kiejtve kapjuk, hogy ${\displaystyle \begin{array}{cc}\hfill {\displaystyle Ri{\text{'}}_1\left(t\right)+L_{11}i\text{'}{\text{'}}_1\left(t\right)+L_{12}i{\text{'}}_2\left(t\right)+\frac{1}{C}{i}_1\left(t\right)=-U_0\omega \text{sin}\omega t\mathrm{,}}\hfill & \text{(<mn>36</mn>)}\\ \hfill {\displaystyle R_{t}i{\text{'}}_2\left(t\right)+L_{22}i\text{'}{\text{'}}_1\left(t\right)+L_{21}i\text{'}{\text{'}}_1\left(t\right)+\frac{1}{C}{i}_2\left(t\right)=0.}\hfill & \text{(<mn>37</mn>)}\end{array}}$ Ebből az egyenletrendszerből $i_1\left(t\right)$-t ki kellene ejteni, de ez közvetlenül lehetetlen. Vegyük észre, hogy ha a megoldásokat (8) mintájára $\begin{array}{c}{\displaystyle i_1\left(t\right)=I_1\text{sin}\left(\omega t+\phi \right)}\end{array}$ (38) és $\begin{array}{c}{\displaystyle i_2\left(t\right)=I\text{sin}\left(\omega t+\phi \right)}\end{array}$ (39) alakban keressük, akkor a (8) és (10) egyenletekből láthatóan az $\begin{array}{c}{\displaystyle i\text{'}{\text{'}}_{1}t=-{\omega }^2{i}_1\left(t\right)}\end{array}$ (40) és az $\begin{array}{c}{\displaystyle i\text{'}{\text{'}}_2\left(t\right)=-{\omega }^2{i}_2\left(t\right)}\end{array}$ (41) összefüggések teljesülnek. Ezekkel könnyen megkaphatjuk a kívánt egyenletet: ${\displaystyle \begin{array}{c}\hfill {\displaystyle R{R}_t{C}^{2}i\text{'}{\text{'}}_2\left(t\right)+\left[\left(1-{\omega }^2{L}_{11}C\right)R_{t}C+\left(1-{\omega }^2{L}_{22}C\right)RC\right]i{\text{'}}_2\left(t\right)+[\left(1-{\omega }^2{L}_{11}C\right)\cdot }\hfill \\ \hfill {\displaystyle \cdot \left(1-{\omega }^2{L}_{22}C\right)-{\omega }^4{L}_{12}^2{C}^2]i_2\left(t\right)+U_0\omega \text{sin}\omega t=0.}\hfill & \text{(<mn>42</mn>)}\end{array}}$ A már ismert technikával kiszámíthatjuk a (39) képletben szereplő $I$, illetve az $U$ feszültség-amplitúdó értékét, illetve a fázisszög tangensét: ${\displaystyle \begin{array}{c}\hfill {\displaystyle U=I{R}_t=}\hfill \\ \hfill {\displaystyle =\frac{U_0{R}_t{L}_{12}{C}^2{\omega }^3}{{\left[\left(1-{\omega }^2{L}_{11}C\right)\left(1-{\omega }^2{L}_{22}C\right)-{\omega }^2{L}_{12}^2{C}^2-{\omega }^{2}R{R}_t{C}^2\right]}^2+{\omega }^2{\left[\left(1-{\omega }^2{L}_{11}C\right)R_{t}C+\left(1-{\omega }^2{L}_{22}C\right)RC\right]}^2}\mathrm{,}}\hfill & \text{(<mn>43</mn>)}\end{array}}$ azaz (15)-höz és (26)-hoz hasonlóan $\begin{array}{c}{\displaystyle U=\frac{\alpha {\omega }^3}{\sqrt[]{{\gamma }_1{\omega }^8+{\gamma }_2{\omega }^6+{\gamma }_3{\omega }^4+{\gamma }_4{\omega }^2+{\gamma }_5}};}\end{array}$ (44) illetve $\begin{array}{c}{\displaystyle \text{tg }\phi =-\frac{\omega \left[\left(1-{\omega }^2{L}_{11}C\right)R_{t}C+\left(1-{\omega }^2{L}_{22}C\right)RC\right]}{\left(1-{\omega }^2{L}_{11}C\right)\left(1-{\omega }^2{L}_{22}C\right)-{\omega }^4{L}_{12}^2{C}^2-{\omega }^{2}R{R}_t{C}^2}\mathrm{.}}\end{array}$ (45) Az $R_t$ ellenálláson megjelenő feszültség a (43) és (45) képletekben adott mennyiségekkel (46) (Több dolgozat alapján)