Feladat:	795. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Dombi Gábor ,  Hordósy Gábor ,  Kerekes János ,  Szamosújvári Sándor ,  Tóth József
Füzet:	1969/április, 185 - 187. oldal		PDF  |  MathML
Témakör(ök):	Pontrendszerek mozgásegyenletei, Nyomóerő, kötélerő, Csúszó súrlódás, Egyenesvonalú mozgás lejtőn, Összetartó erők eredője, Feladat
Hivatkozás(ok):	Feladatok: 1968/november: 795. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.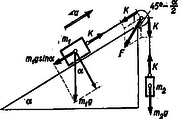   1. ábra   Írjuk fel a mozgásegyenleteket külön-külön az egyes tömegekre az 1. ábra jelölései szerint: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle m_{2}a=m_{2}g-K\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle m_{1}a=K-m_{1}g\cdot \text{sin}\alpha \mathrm{.}}\hfill \end{array}}$ A két egyenletből $\begin{array}{c}{\displaystyle a=\frac{m_2-m_1\text{sin}\alpha }{m_1+m_2}g\mathrm{.}}\end{array}$ A tömeg a lejtőn a) lefelé gyorsul, ha $m_2-m_1\text{sin}\alpha <0$, azaz $\begin{array}{c}{\displaystyle \text{sin}\alpha >\frac{m_2}{m_1}\mathrm{.}}\end{array}$ b) áll vagy egyenletesen mozog, ha $m_2-m_1\text{sin}\alpha =0$, $\begin{array}{c}{\displaystyle \text{sin}\alpha =\frac{m_2}{m_1}\mathrm{.}}\end{array}$ c) fölfelé gyorsul, ha $m_2-m_1\text{sin}\alpha >0$, azaz $\begin{array}{c}{\displaystyle \text{sin}\alpha <\frac{m_2}{m_1}\mathrm{.}}\end{array}$ A kötélerő $\begin{array}{c}{\displaystyle K=\frac{m_1{m}_2}{m_1+m_2}g\left(1+\text{sin}\alpha \right)\mathrm{.}}\end{array}$ A csiga tengelyére az egymással $\left({90}^{\circ }-\alpha \right)$ szöget bezáró $K$ nagyságú erők $F$ eredője hat: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle F=2\cdot K\text{cos}\frac{{90}^{\circ }-\alpha }{2}\mathrm{,}\text{<span style="font-weight: normal;font-style: normal;">vagy átalakítva</span>}}\hfill \\ \hfill {\displaystyle }& {\displaystyle F=\sqrt[]{2}K\cdot \left(\text{cos}\frac{\alpha }{2}+\text{sin}\frac{\alpha }{2}\right)\mathrm{.}}\hfill \end{array}}$ Ha súrlódás van, akkor külön kell megvizsgálnunk az egyes eseteket. 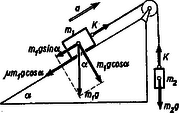    2. ábra   a) Ha $m_1$ felfelé gyorsul, akkor a mozgásegyenletek a következők (2. ábra): 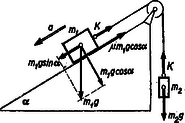${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle m_{2}a=m_2\cdot g-K\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle m_{1}a=K-m_{1}g\left(\text{sin}\alpha +\mu \text{cos}\alpha \right)\mathrm{.}}\hfill \end{array}}$ Így $\begin{array}{c}{\displaystyle a=\frac{m_2-m_1\left(\text{sin}\alpha +\mu \text{cos}\alpha \right)}{m_1+m_2}\cdot g\mathrm{.}}\end{array}$ $\begin{array}{c}{\displaystyle a>\mathrm{0,}\text{<span style="font-weight: normal;font-style: normal;">ha</span>}{m}_2>m_1\left(\text{sin}\alpha +\mu \text{cos}\alpha \right)\mathrm{.}}\end{array}$ Egyenlőség esetén $m_1$ a lejtőn áll, vagy egyenletesen mozog felfelé.     3. ábra   b) Ha $m_1$ lefelé gyorsul (3. ábra) ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle m_{2}a=m_{2}g-K\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle m_{1}a=m_{1}g\left(\text{sin}\alpha -\mu \text{cos}\alpha \right)-K\mathrm{.}}\hfill \end{array}}$ Ekkor $\begin{array}{c}{\displaystyle a=\frac{m_1\left(\text{sin}\alpha -\mu \text{cos}\alpha \right)-m_2}{m_1+m_2}\cdot g\mathrm{.}}\end{array}$ $\begin{array}{c}{\displaystyle a>\mathrm{0,}\text{<span style="font-weight: normal;font-style: normal;">ha</span>}{m}_1\left(\text{sin}\alpha -\mu \text{cos}\alpha \right)>m_2\mathrm{.}}\end{array}$ Egyenlőség esetén $m_1$ a lejtőn áll, vagy egyenletesen mozog lefelé. Előfordulhat, hogy egyik feltétel sem teljesül, azaz $\begin{array}{c}{\displaystyle m_1\left(\text{sin}\alpha -\mu \text{cos}\alpha \right)<m_2<m_1\left(\text{sin}\alpha +\mu \text{cos}\alpha \right)\mathrm{.}}\end{array}$ Ekkor a test semmilyen irányban sem tud elmozdulni.     Dombi Gábor (Szeged, Ságvári E. Gyak. Gimn., III. o .t .)