Kezdőlap


Feladat:	787. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Gyimesi Ferenc , Horváthy Péter , Mihály György , Ormos Pál , Szamosújvári Sándor
Füzet:	1969/március, 140 - 141. oldal		PDF \| MathML
Témakör(ök):	Hajítások, Rugalmatlan ütközések, Ütközés fallal, Feladat
Hivatkozás(ok):	Feladatok: 1968/október: 787. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) A részecske pályája az ütközés előtt és után egy-egy ferde hajítási pályaszakaszból áll.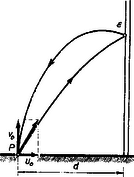

Mivel ütközéskor a függőleges sebesség nem változik, ezért a teljes repülési idő

T = 2 v_{0} / g

. A részecske vízszintesen

u_{0}

sebességgel

d

utat tesz meg a falig

t_{1} = d / u_{0}

idő alatt. Ütközéskor a sebesség vízszintes komponensének nagysága

ε u_{0}

lett. Így a

P

-be visszajutás ideje

t_{2} = d / (ε u_{0})

. Nyilván

T = t_{1} + t_{2}

. Behelyettesítve

\begin{matrix} \frac{2 v_{0}}{g} & = \frac{d}{ε u_{0}} + \frac{d}{u_{0}}, ebből \\ u_{0} v_{0} & = \frac{(1 + ε) g d}{2 ε} . & (1) \end{matrix}

b) A mozgás két szakasza közül az ütközés utáni a hosszabb idejű, hiszen a részecske kisebb vízszintes sebességgel ugyanazt az utat teszi meg. Mivel az ütközés a részecske függőleges mozgását nem befolyásolja, így legmagasabban

t = v_{0} / g

félidőben van, azaz az ütközés után. Ezután még

v_{0} / g

ideig mozog

ε u_{0}

vízszintes sebességgel, míg

P

-be ér, így a csúcs

s = ε u_{0} v_{0} / g

távolságra van

P

-től. Az előző eredmény felhasználásával a faltól való távolság

\begin{matrix} l = d - s = d - (1 + ε) d / 2 = (1 - ε) d / 2, \end{matrix}

ami csak

d

-től és

ε

-tól függ.
c) A kezdősebesség komponenseit a kezdősebesség

v

nagyságával és a vízszintessel bezárt

α

szögével kifejezve

\begin{matrix} v_{0} = v sin α; u_{0} = v cos α . (1) -ből \end{matrix}

u_{0} v_{0} = v^{2} sin α cos α = v^{2} (sin 2 α) / 2 = konst

.
Látszik, hogy

v

akkor a legkisebb, amikor

sin 2 α

legnagyobb, azaz mikor

α = 45^{\circ}

a kilövési szög. Ekkor

u_{0} = v_{0} = v / \sqrt[]{2}

.
(1) alapján kapjuk, hogy

v = \sqrt[]{\frac{(1 + ε) g d}{ε}}

.
Mivel

s

értéke

0

és

1

között változhat,

v

akkor minimális, ha

ε = 1

. Ez a teljesen rugalmas ütközés esete.

Ormos Pál (Szeged, Radnóti M. Gimn., III. o. t.)