Kezdőlap


Feladat:	771. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Balogh Gábor , Maróti Péter , Tél Tamás
Füzet:	1969/február, 87 - 89. oldal		PDF \| MathML
Témakör(ök):	Rugalmas erő, Rugalmas energia, Energiamegmaradás tétele, Egyéb körmozgás, Feladat
Hivatkozás(ok):	Feladatok: 1968/május: 771. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vizsgáljuk először azt az esetet, amikor a golyó a körpályán tartózkodik. A testre hat az $m g$ nehézségi erő, a rugó $F_{r} = D Δ l$ húzóereje és a körpálya $F_{n}$ reakcióereje.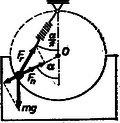

1. ábra

Az előbbi kettőt felbontva sugárirányú és érintőleges komponensekre, majd az összegzést elvégezve, az eredő sugárirányú, ill. érintőleges erő:

\begin{matrix} F_{1} & = F_{n} + F_{r} cos α / 2 - m g cos α, & (1) \\ F_{2} & = m g sin α - F_{r} sin α / 2. & (2) \end{matrix}

Itt ‐ amíg a golyó körpályán mozog, ‐

F_{1}

adja a centripetális erőt:

\begin{matrix} F_{1} = m \frac{v^{2}}{r} . \end{matrix}

(3)

A test elengedésekor

F_{r} = 0

F_{2} = m g sin α

‐ s ennek hatására megindul a körpályán lefelé, fokozatosan növekvő sebességgel. De ez a rugó megnyúlását vonja maga után, amelynek kettős hatása van: egyrészt visszafelé húzza a testet, másrészt igyekszik a pályáról leemelni. A test sebessége a mechanikai energiamegmaradás elve alapján számítható:

\begin{matrix} m g Δ h = \frac{m v^{2}}{2} + \frac{1}{2} D Δ l^{2}, \end{matrix}

a helyzeti energia egy része mozgási és rugóenergiává alakul. Innen

\begin{matrix} v^{2} = 2 g Δ h - \frac{D Δ l^{2}}{m} . \end{matrix}

Behelyettesítve a

\begin{matrix} Δ h & = r (cos α - cos α_{0}), \\ Δ l & = 2 r (cos α / 2 - cos α_{0} / 2) \end{matrix}

értéket:

\begin{matrix} v = \sqrt[]{2 r [g (cos α - cos α_{0}) - \frac{2 D r}{m} {(cos \frac{α}{2} - cos \frac{α_{0}}{2})}^{2}]} . \end{matrix}

(4)

Nyugalmi helyzet nem jöhet létre, s ezt a következőképpen láthatjuk be.
A testre ható erők eredője csak a rugó és súlyerővektorok által közbezárt szögtartományban lehet. Ha az eredő az

O X

és a súlyerő közötti tartományba esik

(F)

, akkor érintőleges összetevője a testet lefelé gyorsítja, nyugalom nem lehet. Ha ez nem teljesül, akkor viszont az eredő

(F')

sugárirányú komponense a testet

O

felé húzza, s előbb leemeli a pályáról, mintsem hogy az megállhatna; ez akkor következik be, amikor a csökkenő sebességnek (hiszen most

F'

érintőleges összetevője lassít!) megfelelő

m v^{2} / r

centripetális erő kisebb lesz a kérdéses összetevőnél.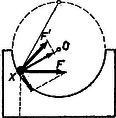

2. ábra

Annak a feltétele, hogy a rugó ne emelje le a golyót a pályáról, az, hogy az

(1)

-ből kifejezett

F_{n}

nyomóerő

\geq 0

legyen:

\begin{matrix} F_{1} - m g cos α - F_{r} cos α / 2 \geq 0. \end{matrix}

Betéve

F_{1}

és

F_{r}

értékét:

\begin{matrix} \frac{m v^{2}}{r} + m g cos α \geq 2 D r (cos \frac{α}{2} - cos \frac{α_{0}}{2}) cos \frac{α}{2} . \end{matrix}

Ide

(4)

-ből

v^{2}

-et behelyettesítve megkapjuk

α

-ra a pályán maradás feltételét:

\begin{matrix} 6 cos^{2} \frac{α}{2} (m g - D r) + 10 cos \frac{α}{2} cos \frac{α_{0}}{2} D r - 4 cos^{2} \frac{α_{0}}{2} (m g + D R) - m g \geq 0. \end{matrix}

D r

-rel osztva, s bevezetve az

a = \frac{m g}{D r}

jelölést, látjuk, hogy

α

és

α_{0}

értéke határozza meg a mozgás lefolyását:

\begin{matrix} 6 cos^{2} \frac{α}{2} (a - 1) + 10 cos \frac{α}{2} cos \frac{α_{0}}{2} - 4 cos^{2} \frac{α_{0}}{2} (a + 1) - a \geq 0. \end{matrix}

(5)

(5)

megoldása

\begin{matrix} a > 1 esetén: & cos \frac{α}{2} \geq \frac{A - 5 cos α_{0} / 2}{6 (a - 1)}, \\ a < 1 esetén: & \frac{5 cos α_{0} / 2 - A}{6 (1 - a)} \leq cos \frac{α}{2} \frac{5 cos α_{0} / 2 + A}{6 (1 - a)}, & (6) \\ a = 1 esetén: & cos \frac{α}{2} \leq \frac{8 cos^{2} α / 2 + 1}{10 cos α_{0} / 2}, \end{matrix}

ahol

\begin{matrix} A = \sqrt[]{a^{2} (24 cos^{2} α_{0} / 2 + 6) - 6 a + cos^{2} α_{0} / 2} . \end{matrix}

Amíg

α

eleget tesz a

(6)

egyenlőtlenségeknek, a golyó a körpályán marad. Ellenkező esetben lelép róla; s további mozgását leírni nem tudjuk (pontról-pontra változó görbületi sugarú pálya ‐ s így a centripetális erőt nem tudjuk kiszámítani ‐ lásd az 1965. évi tanulmányi verseny II. fordulójának 1. feladatát: KML 1965. év 7. sz. 82. o.), de ez nem is célunk.

Adataink esetén:

(6)

-ból

0, 8 < cos α / 2 < 2, 1

adódik, ami

0 \leq α \leq 60^{\circ}

esetén mindig teljesül, tehát a golyó a mélypontig a körpályán marad. A túlsó oldalon felfelé menet teljesen hasonlóan mozog, olyan magasra és fel, mint amilyenről indult, majd ismét lefelé indul, s csillapítatlan lengéseket végez (az energiaveszteségeket elhanyagoltuk).

(6)

-ból most

0, 722 < cos α / 2 < 0, 982

, ebből

21, 8^{\circ} < α < 87, 6^{\circ}

tehát

a_{k} \approx 21, 8^{\circ}

kritikus szögnél a rugó leemeli a körpályáról a testet, amely eddig azon mozgott.

Maróti Péter (Szeged, Ságvári E. g. III. o. t.) és
Tél Tamás (Bp., Apáczai Csere J. III. o. t.)
dolgozata alapján, kiegészítésekkel

Megjegyzések. 1. Több dolgozat szerzője indokolatlanul feltételezte, hogy a test végig a pályán marad, ha a mélyponton az

(5)

vagy ennek megfelelő más alakú egyenlet teljesül. Ez általában nem igaz, pl. ha

a = 0, 5

α = 90^{\circ}

, akkor

0, 74 < cos α / 2 < 1, 6

, s ebből

0 \leq α < 84, 6^{\circ}

, amit az

α = 0

mélypont kielégít, pedig a golyó rögtön az induláskor elhagyja a pályát.

2. Balogh Gábor (Bp., Radnóti M. g., III. o. t.) megkísérelte a 2. adatrendszer esetén a golyó pályájának meghatározását a körpálya elhagyása után, pontról-pontra közelítő számítással, s az eredményt grafikonon tüntette fel.