Kezdőlap


Feladat:	745. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bodor Géza , Gerhardt Tamás , Harmat Péter
Füzet:	1968/november, 179 - 181. oldal		PDF \| MathML
Témakör(ök):	Erők forgatónyomatéka, Súlypont (tömegközéppont) meghatározása, Geometriai szerkesztések alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1968/február: 745. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az adott lécek hossza $L$ és legyenek egymáshoz képest $φ$ szögben összeerősítve (1. ábra).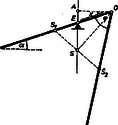

1. ábra

Az ék legyen

x

távolságra a lécek

O

összeerősítési pontjától. A szerkezet

S

súlypontja a lécek középpontjait összekötő egyenes felében van. Egyensúlyi helyzetben

S

súlypontnak az ék alatt kell lennie. Ekkor a bal oldali léc felfelé mérve

α

szöget zár be a vízszintessel.

S_{1} O = S_{2} O = L / 2

.
Az

A O

távolságot kifejezzük az

E O A

, valamint az

S O A

háromszögből:

\begin{matrix} A O & = x cos α, \\ A O & = S O \cdot cos (α + φ / 2) = \frac{L cos (φ / 2) cos (α + φ / 2)}{2} . \end{matrix}

Ezeket egyenlővé téve és rendezve:

\begin{matrix} \frac{x}{L} = \frac{cos (φ / 2) cos (α + φ / 2)}{2 cos α} . \end{matrix}

(1)

Ez a képlet adja meg, hogy adott

L

φ

mellett hogyan függ az ék helyét meghatározó

x / L

hányados a léc elhelyezkedését megadó

α

szögtől.

Gerhardt Tamás (Bp., Kaffka M. g. II. o. t.)

II. megoldás. A két léc

S_{1}

és

S_{2}

súlypontjaiban ható erők egyenlők, tehát az erőkaroknak is egyenlőknek kell lenniök (2. ábra).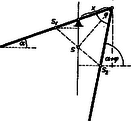

2. ábra

S_{1}

-ben ható súlyerő karja:

(L / 2 - x) cos α

,
Az

S_{2}

-ben ható súlyerő karja:

x cos α - L cos (α + φ) / 2

.
Ezeket egyenlővé tesszük:

\begin{matrix} (L / 2 - x) cos α = x cos α - L cos (α + φ) / 2. \end{matrix}

Ezt az egyenletet

x / L

-re rendezve az előbbi (1) alatti eredményt kapjuk.

Bodor Géza (Bp., Jedlik Á. g. II. o. t.)

III. megoldás. Szerkesztéssel következőképp járunk el (3. ábra).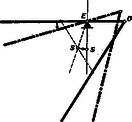

3. ábra

Adva van az ék helye

E O = x

által. Először felrajzoljuk a léceket úgy, hogy a bal oldali léc vízszintes legyen, azután az egész szerkezetet elforgatjuk azzal a szöggel, amelyet az

S E

egyenes a függőlegessel bezár. Így kapjuk meg az egyensúlyi helyzetet (eredményvonallal jelölve).

Harmat Péter (Mosonmagyaróvár, Kossuth L. g. II. o. t.)

Megjegyzések. Zavaró, hogy (1) képletünk az

x / L

ékhelyzetet adja meg

α

függvényeként és nem fordítva. Ha ismerjük az összeg cosinusának képletét:

\begin{matrix} cos (γ + δ) = cos γ cos δ - sin γ sin δ, \end{matrix}

akkor (1) képletünkben ezt felhasználhatjuk:

\begin{matrix} \frac{x}{L} & = \frac{cos φ / 2}{2 cos α} \cdot (cos α cos φ / 2 - sin α sin φ / 2), \\ \frac{2 x}{L} & = cos^{2} (φ / 2) - tg α sin (φ / 2) cos (φ / 2), \end{matrix}

innen:

\begin{matrix} tg α = \frac{cos^{2} (φ / 2)}{sin (φ / 2) cos (φ / 2)} - \frac{2}{sin (φ / 2) cos (φ / 2)} \cdot \frac{x}{L} . \end{matrix}

Felhasználhatjuk a kétszeres szög sinusát ebben az alakban:

\begin{matrix} sin 2 \cdot φ / 2 = 2 sin (φ / 2) cos (φ / 2) . \end{matrix}

Így megkapjuk, miként függ a helyzetet megadó

α

szög az ék

x / L

helyétől:

\begin{matrix} tg α = ctg \frac{φ}{2} - \frac{4}{sin φ} \cdot \frac{x}{L} . \end{matrix}

(2)

4. ábránk megmutatja

φ = 60^{\circ}

90^{\circ}

120^{\circ}

mellett

α

értékeit

x / L

függvényeként.

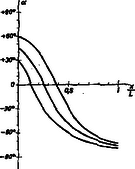4. ábra

Negatív

α

lelógó lécet jelent. Az 5. ábránk ugyanezeknél a léceknél néhány jellegzetes egyensúlyi helyzetet mutat meg.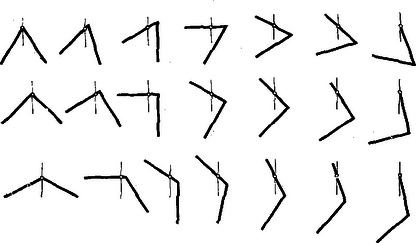

5. ábra

Tulajdonképp

x / L

számára csak

0

és

1

közötti értékek értelmesek,

0 \leq x / L \leq 1

, de ha a bal oldali lécen kétoldalt valamiféle súlytalan, szilárd meghosszabbítást képzelünk el, akkor (2) képletünkből ezekre az esetekre is választ kaphatunk. Negatív

x / L

esetében

α

mindjobban

+ 90^{\circ}

-hoz,

1

-nél nagyobb

x / L

mellett

- 90^{\circ}

-hoz közeledik.

φ = 0^{\circ}

mellett (összecsukott léc)

x / L = 0, 5

-nél

α = 0^{\circ}

, minden ennél kisebb

x / L

-nél

α = + 90^{\circ}

, ennél nagyobb

x / L

-nél

α = - 90^{\circ}

φ = 180^{\circ}

mellett (teljesen kinyitott léc)

x / L = 0

-nál

α = 0^{\circ}

, minden egyéb pozitív

x / L

-nél

α = - 90^{\circ}

.
A (2) képlettel egyenlő értékű eredmények vezethetők le a cosinus-tétel felhasználásával is.