Kezdőlap


Feladat:	708. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Herneczki István , Takács László
Füzet:	1968/április, 178 - 181. oldal		PDF \| MathML
Témakör(ök):	Rögzített tengely körüli forgás (Merev testek mozgásegyenletei), Harmonikus rezgőmozgás, Analógia alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1967/szeptember: 708. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a korong kitérésének szöge az egyensúlyi helyzetből $φ$ (1. ábr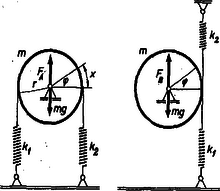a).

1. ábra

Mivel a fonál csak egy irányban képes erőt továbbítani, vagyis csak húzni tud, a feladatban külön kell tárgyalni a két esetet:

\begin{matrix} 1) φ \geq 0, 2) φ \leq 0. \end{matrix}

Először az első esetet vizsgáljuk.
Ha

φ \geq 0

, akkor csak a

k_{2}

direkciós erejű rugó fejt ki forgatónyomatékot. Ez a forgatónyomaték:

\begin{matrix} M = - (k_{2} r φ) r . \end{matrix}

A forgómozgás alapegyenletéből:

\begin{matrix} Θ β = - (k_{2} r φ) r, \end{matrix}

ahol

Θ = (1 / 2) m r^{2}

a tehetetlenségi nyomaték és

β

a szöggyorsulás. Rendezés után azt kapjuk, hogy

\begin{matrix} β = - 2 (k_{2} / m) φ . \end{matrix}

Az ingamozgás levezetésénél ehhez az egyenlethez hasonló egyenletet kaptunk. Ha összehasonlítjuk a két egyenletet, akkor ennek a rezgőmozgásnak a periódusidejére

\begin{matrix} T_{2} = 2 π \sqrt[]{\frac{m}{2 k_{2}}} \end{matrix}

kifejezést kapunk.
Ha

φ \leq 0

, a megoldás teljesen hasonlóan megy, így

\begin{matrix} T_{1} = 2 π \sqrt[]{\frac{m}{2 k_{1}}} . \end{matrix}

Mivel mind a két esetben csak egy fél periódust tesz meg a test, a rendszer mozgásának periódusideje

\begin{matrix} T = π \sqrt[]{\frac{m}{2}} (\frac{1}{\sqrt[]{k_{1}}} + \frac{1}{\sqrt[]{k_{2}}}) . \end{matrix}

Most kiszámítjuk a csapágyban ébredő kényszererő függését az időtől. Ehhez kell a rezgőmozgás megoldása.
Ha

φ \geq 0

, akkor a kitérés

x = A sin ω_{2} t

, ahol

\begin{matrix} ω_{2} = \frac{2 π}{T_{2}} \end{matrix}

(1)

és ha

φ \leq 0

, akkor

\begin{matrix} x = B sin ω_{1} t \end{matrix}

(2)

2. ábra

φ

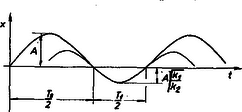éppen a szinuszfüggvény argumentumában szereplő

ω_{1} t

, ill.

ω_{2} t

kifejezés.
A rezgőmozgás sebessége

φ = 0

esetre az (1) adatokkal

A ω_{2}

, a (2) adatokkal

A ω_{1}

. Ezek egyenlőségéből

\begin{matrix} β = A \frac{ω_{1}}{ω_{2}} = A \frac{T_{2}}{T_{1}} = A \sqrt[]{\frac{k_{1}}{k_{2}}} . \end{matrix}

Tehát a megoldások:

\begin{matrix} ha & φ \geq 0, x = A sin ω_{2} t, \\ φ \leq 0, x = A \sqrt[]{k_{1} / k_{2}} sin ω_{1} t . \end{matrix}

A második elrendezésre a rezgőmozgás számítása ugyanaz, mivel a forgatónyomatékok azonosak az első esettel.
Az erők egyensúlyából határozzuk meg a csapágyra ható erőket. A csapágyat a súlyerőn kívül még a rugó is húzza. Így ezek az erők az első elrendezésre:

\begin{matrix} ha & φ \geq 0, F_{A} = m g + k_{2} x = m g + A k_{2} sin ω_{2} t, \\ φ \leq 0, F_{A} = m g + k_{1} x = m g + A k_{1} \sqrt[]{k_{1} / k_{2}} sin ω_{1} t . \end{matrix}

A második elrendezésre:

\begin{matrix} φ \geq 0, F_{B} = m g + k_{2} x = m g + A k_{2} sin ω_{2} t, \\ φ \leq 0, F_{B} = m g - k_{1} x = m g - A k_{1} \sqrt[]{k_{1} / k_{2}} sin ω_{1} t . \end{matrix}

Nézzük azt az esetet, amikor az egyik rugó, a

k_{1}

direkciós erejű, meg van feszítve

x_{1}

-gyel. Ekkor egyensúlyban a forgatónyomatékok egyenlőségéből

\begin{matrix} k_{1} x_{1} r = k_{2} x_{2} r, \end{matrix}

tehát a másik rugó megnyúlása

x_{2} = x_{1} \frac{k_{1}}{k_{2}}

.
Ha a kitérésre

(φ r)

a következő egyenlőtlenség áll fenn:

\begin{matrix} - x_{2} \leq (φ r) \leq x_{1}, \end{matrix}

akkor az egész mozgás alatt mindkét rugó feszített állapotban van. Az előző megoldáshoz hasonlóan most

\begin{matrix} Θ β = - (k_{1} + k_{2}) r^{2} φ, \end{matrix}

és ebből

\begin{matrix} T = 2 π \sqrt[]{\frac{Θ}{(k_{1} + k_{2}) r}} = 2 π \sqrt[]{\frac{m}{2 (k_{1} + k_{2})}} . \end{matrix}

Az erő pedig az első (A) esetben:

\begin{matrix} F_{A} = m g + k_{1} (x_{1} - x) + k_{2} (x_{2} + x), \end{matrix}

ahol

x = A sin ω t, (ω = \frac{2 π}{T})

.
A második (B) esetben:

\begin{matrix} F_{B} = m g - k_{1} (x_{1} + x) + k_{2} (x_{2} - x) . \end{matrix}

Ha az egyik vagy mindkét kitérés túllépi a kritikus

x_{1}

, ill.

x_{2}

értéket, akkor a helyzet bonyolultabb, mert a mozgást három rezgőmozgásból kell összetenni, aszerint, hogy

\begin{matrix} 1. x_{1} \leq (φ r), \\ 2. - x_{2} \leq (φ r) \leq x_{1}, \\ 3. (φ r) \leq - x_{2} \end{matrix}

áll-e fenn. E megoldásoknál teljesülnie kell annak, hogy a

φ r = x_{1}

helyen az 1. és 2. megoldás,

φ r = x_{2}

helyen a 2. és 3. megoldás ugyanazt a sebességet adja. A 3. ábra mutat egy ilyen megoldást.

3. ábra

Az ilyen módon kapott kitérésekből a csapágyra ható erőket az előzőek alapján kell meghatározni.

Herneczki István (Sopron, Széchenyi I. g. IV. o. t.)
Takács László (Sopron, Széchenyi I. g. IV. o. t.) dolgozata alapján