Feladat: 704. fizika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Gyimesi Ferenc ,  Horváthy Péter ,  Lakatos Éva 
Füzet: 1968/február, 94 - 96. oldal  PDF  |  MathML 
Témakör(ök): Súlypont (tömegközéppont) meghatározása, Feladat
Hivatkozás(ok):Feladatok: 1967/szeptember: 704. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Foglalkozzunk először az általános esettel.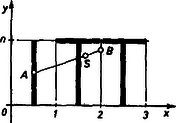

 

 

1. ábra
 

Az 1. ábrán látható koordináta-rendszerben az egyes betűk súlypontjának koordinátái a következők: Az I betű súlypontja a magasság felében lesz: A(1/2;n/2). A két T betűre
(3/2;n2+2n2n+1),illetve(5/2;n2+2n2n+1)
adódik. (A függőleges és vízszintes szárból álló egész test súlypontját a két szár súlypontjának koordinátáiból számoltuk ki. A két T betűnek mint egy testnek súlypontja a fenti két adatból könnyen kapható, a magasság ugyanaz, a ,,súlyok'' egyenlők, ezért az x koordináták számtani középarányosa lesz a súlypont abszcisszája:
B(2;n2+2n2n+1).

Az A súlypontú test tömege n egység, a B súlypontúé pedig (2n+2) egység. Az egész test súlypontja az AB szakaszon van és azt a tömegekkel fordított arányban osztja. Így S koordinátáira a következő értékek adódnak:
x=9n+82(3n+2),y=3n2+4n2(3n+2).

Az első kérdésre az n=1 helyettesítéssel kapjuk a választ:
x=1,7,y=0,7.

Az S súlypont pályájának egyenletét úgy kapjuk meg, ha x és y kifejezéséből kiküszöböljük az n paramétert:
y=4(2-x)⋅(x-1)3(2x-3).

Megvizsgálva két speciális esetet: n=0, azaz y=0 esetén x=2, ekkor csak a T betűk vízszintes szára marad meg. Ha n értékét egyre növeljük, y értéke is ∞ felé tart. Tehát 1/y, nullához közeledik, ezért a fenti törtkifejezés reciprokát tekintve ‐ az tart 0-hoz. Így ‐ annak nevezője korlátos lévén ‐ a számlálója is tart 0-hoz.
Tehát 2x-3→0, azaz x→3/2. A súlypont tehát egyre közeledik az első T betű szárához. A növekvő súlyú függőleges szárak egyre növekvő mértékben hatnak a súlypont helyzetére.
 

Lakatos Éva (Bp., VIII., Százados úti g. II. o. t.)
 

II. megoldás. Vegyünk fel egy derékszögű koordináta-rendszert a 2. ábrán látható módon.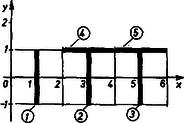
 

 

2. ábra
 

A betűket alkotó egyes egyenesszakaszok koordinátái xi,yi. A súlypont koordinátáit az egyes elemek súlypont-koordinátáinak súlyozott átlaga adja. Egy-egy betűszár fél hosszát és teljes súlyát egységnyinek tekintjük.
m1=m2=...=m5=1,x1=1,x2=3,x3=5,x4=3,x5=5,y1=y2=y3=0,y4=y5=1.


Így a tömegekkel súlyozott átlag
X=m1x1+m2x2+...+m5x5m1+m2+...+m5=1⋅1+2⋅3+2⋅55=3,4.
Hasonlóan
Y=0⋅3+1⋅25=0,4.
Ha a függőleges szárakat n-szeresre növeljük, akkor
X=n⋅1+n⋅3+n⋅5+1⋅3+1⋅53n+2=9n+83n+2;Y=n⋅0+n⋅0+n⋅0+1⋅n+1⋅n3n+2=2n3n+2.
Ha n=0, akkor x=4, y=0. Ha n nő, akkor x monoton csökken, y monoton növekszik. Ha n→∞, akkor x→3 és y→2/3.
A súlypont pályájának egyenlete n kiküszöbölése után
y=-23x+83.
A pálya egyenlete egy egyenes egyenlete és csak az előbb meghatározott n=0 és n=∞ esetén felvett (4,0) és (3,23) pontok között értelmezhető.
Horváthy Péter (Bp., Fazekas M. g. II. o. t.)
 

Megjegyzés. Az első pillanatban furcsának tűnhet, hogy egyszerű koordináta-rendszer eltolás miatta pálya hiperbolából egyenessé alakul. Figyeljük meg azonban, hogy az első megoldásbeli koordináta-rendszerhez viszonyítva a második megoldásbeli koordináta-rendszer mozog, ha n változik, a függőleges szárak súlypontjával együtt.
Hiperbolikus, de más alakú pályaegyenletet kapunk, ha a T betűk vízszintes szárához rögzítjük az x tengelyt, mint az például Gyimesi Ferenc (Győr, Révai M. g. II. o. t.) megoldásában található (3. ábra):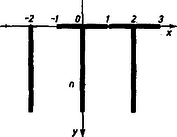
X=23n+2,Y=3n23n+2;Y=23(X+1X)-43.



 

3. ábra