Kezdőlap


Feladat:	689. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Battha László , Berkes Zoltán , Ferenczi János
Füzet:	1968/február, 88 - 90. oldal		PDF \| MathML
Témakör(ök):	Sikkondenzátor, Kondenzátorok párhuzamos kapcsolása, Egyéb változó áram, Feladat
Hivatkozás(ok):	Feladatok: 1967/április: 689. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vezessük be a következő jelöléseket! A kondenzátorok kapacitása $C_{1} = 1$ pF és $C_{2} = 1,5$ pF, a lemezek távolsága a kezdő pillanatban $d_{1} = 20$ cm és $d_{2} = 20$ cm. A kondenzátorokban levő össztöltés $Q = 0, 1$ C. A lemezek távolodási sebessége $v_{1}$ és $v_{2}$ (közeledés esetén $v$ negatív szám).
Határozzuk meg $t$ időpillanatban az egyes kondenzátorokon levő töltést ! A párhuzamosan kapcsolt kondenzátorok feszültsége:

\begin{matrix} U (t) = \frac{Q_{1} (t)}{C_{1} (t)} = \frac{Q_{2} (t)}{C_{2} (t)} . \end{matrix}

Az elektromos töltés megmaradása miatt az össztöltés mindvégig

\begin{matrix} Q = Q_{1} (t) + Q_{2} (t) . \end{matrix}

Mivel a síkkondenzátor kapacitása

C = k \frac{F}{d}

alakban írható (

F

a lemezek felszíne), ezért

\begin{matrix} C_{1} (t) = C_{1} \frac{d_{1}}{d_{1} + v_{1} t} és C_{2} (t) = C_{2} \frac{d_{2}}{d_{2} + v_{2} t}, \end{matrix}

Az egyenletrendszert megoldva:

\begin{matrix} Q_{1} (t) = Q \frac{\frac{C_{1} d_{1}}{d_{1} + v_{1} t}}{\frac{C_{1} d_{1}}{d_{1} + v_{1} t} + \frac{C_{2} d_{2}}{d_{2} + v_{2} t}} és Q_{2} (t) = Q \frac{\frac{C_{2} d_{2}}{d_{2} + v_{2} t}}{\frac{C_{1} d_{1}}{d_{1} + v_{1} t} + \frac{C_{2} d_{2}}{d_{2} + v_{2} t}} . \end{matrix}

A kérdés az, hogy milyen erősségű áramnak kellett az egyes pillanatokban folynia ahhoz, hogy a

t

pillanatban a

C_{1}

kondenzátoron

Q_{1} (t)

töltés legyen. Erre a kérdésre a felelet megadása kb. olyan nehéz, mint változó sebességű mozgás esetén a pillanatnyi sebességnek az út-idő függvényből való meghatározása. Sőt ez a hasonlóság olyan szoros, hogy itt is lényegében ugyanazt a módszert alkalmazhatjuk. Először a pillanatnyi áramerősség helyett azt határozzuk meg, hogy a

t

és

t + Δ t

időpillanatok között milyen

\bar{I (t)}

átlag áram növelte volna a

t

pillanatbeli

Q_{1} (t)

töltést a

t + Δ t

pillanatbeli

Q_{1} (t + Δ t)

-re. Mivel az áramerősség az időegységnyi idő alatt szállított töltés mennyisége, ezért

Δ t

idő alatt:

\begin{matrix} Δ Q = Q_{1} (t + Δ t) - Q_{1} (t) = \bar{I (t} \cdot Δ t; \end{matrix}

ebből

\begin{matrix} \bar{I (t)} = \frac{Δ Q}{Δ t} = (\frac{Q}{1 + \frac{C_{2} d_{2}}{C_{1} d_{1}} \cdot \frac{d_{1} + v_{1} (t + Δ t)}{d_{2} + v_{2} (t + Δ t)}} - \frac{Q}{1 + \frac{C_{2} d_{2}}{C_{1} d_{1}} \cdot \frac{d_{1} + v_{1} t}{d_{2} + v_{2} t}}) \frac{1}{Δ t} . \end{matrix}

Behelyettesítve a numerikus értékeket:
a) Ha a

C_{1}

kondenzátor lemezeit közelítjük, ekkor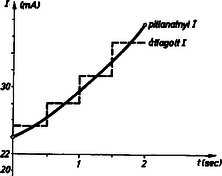

v_{1} = - 10

cm/s és

v_{2} = + 10

cm/s.

\begin{matrix} \bar{I (t)} = \frac{2, 4}{(10 - t) (10 - t - Δ t)} A . \end{matrix}

1. ábra

Az 1. ábrán látható, hogy

Δ t = 0, 5

s esetén az egyes intervallumokban milyen átlag áramerősségeket kapunk. A pillanatnyi áramerősségeket azonban ez a lépcsős görbe nem adja meg helyesen, de ha kisebb

Δ t

értéket veszünk, akkor a vizsgált idő alatt kisebb lesz az áramerősség megváltozása, ezért az átlagérték közelebb lesz a pillanatnyi értékhez. Határesetben

Δ t = 0

, az ekkor kapott értéket tekinthetjük a pillanatnyi áramerősségnek:

\begin{matrix} I (t) = \frac{2, 4}{{(10 - t)}^{2}} A . \end{matrix}

b) Ha a

C_{2}

lemezei közelednek:

v_{1} = + 10

cm/s és

v_{2} = - 10

cm/s. Ekkor a

t

és

t + Δ t

között az átlagos áram: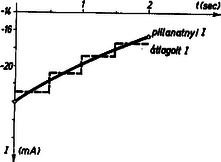

\begin{matrix} \bar{I (t)} = \frac{- 2, 4}{(10 + t) (10 + t + Δ t)} A . \end{matrix}

2. ábra

A pillanatnyi áram (2. ábra):

\begin{matrix} I (t) = - \frac{2, 4}{{(10 + t)}^{2}} A . \end{matrix}

A ,,

-

'' előjel mutatja, hogy ekkor a töltések

C_{1}

-ből a

C_{2}

-be áramlanak.
Battha László (Bp., Eötvös J. g. IV. o. t.)

Megjegyzés. A feladat nem reális. A fenti adatok mellett megvalósítása lehetetlen.

1

pF kapacitás

0, 1

C töltés esetén

10^{11}

volt feszültséget jelent, továbbá a tér sem lehet homogén. Erre egyik megoldó sem mutatott rá.