Kezdőlap


Feladat:	682. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Kürti Gábor , Takács László
Füzet:	1968/január, 42 - 44. oldal		PDF \| MathML
Témakör(ök):	Rugalmatlan ütközések, Gördülés vízszintes felületen, Csúszó súrlódás, Feladat
Hivatkozás(ok):	Feladatok: 1967/március: 682. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Foglalkozzunk az általános esettel. Tartozzon a kezdetben guruló golyóhoz az 1., az eredetileg állóhoz a 2. index. A golyók kerületi sebességei a középponthoz viszonyítva $ω_{1} r$ és $ω_{2} r$ . A tehetetlenségi nyomatékok $I_{1} = Φ m_{1} r^{2}$ és $I_{2} = Φ m_{2} r^{2}$ , $(Φ = 0, 4$ gömbnél). Az ún. tömeghányadok:

\begin{matrix} k = \frac{m_{1}}{m_{1} + m_{2}}, 1 - k = \frac{m_{2}}{m_{1} + m_{2}} . \end{matrix}

Az ütközés előtti állapotban (

a

indexszel jelölve)

v_{1 a} = v_{0}

v_{2 a} = 0

ω_{1 a} r = v_{0}

ω_{2 a} r = 0

. Foglalkozzunk először azzal az esettel, amikor

μ_{1} m_{1} < μ_{2} m_{2}

: A sebességek időtől való függését az 1. ábra mutatja.

1. ábra

Közvetlenül az ütközés pillanatában (

b

)

v_{1 b} = v_{2 b} = k v_{0}

;

ω_{1 b} r = v_{0}

ω_{2 b} r = 0

. Ezután (

c

‐állapot) az első golyó forgását a súrlódás fékezi

μ_{1} m_{1} g

erővel, a második golyó forgása a súrlódás következtében gyorsul, itt a súrlódási erő

μ_{2} m_{2} g

. Hozzá véve az első golyó középpontjában

\pm μ_{1} m_{1} g

, a második golyó középpontjában

\pm μ_{2} m_{2} g

erőket (2. ábra), a két golyó középpontjait együttesen

(μ_{2} m_{2} - μ_{1} m_{1}) g

erő

(μ_{2} m_{2} - μ_{1} m_{1}) g / (m_{1} + m_{2})

gyorsulással lassítja, tehát az együtt maradó golyók centrumainak sebessége: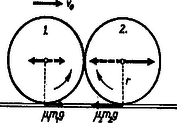

\begin{matrix} v_{1 c} = v_{2 c} = k v_{0} - \frac{μ_{2} m_{2} - μ_{1} m_{1}}{m_{1} + m_{2}} \cdot g \cdot t . \end{matrix}

2. ábra

Az első golyó forgása lassul, a másodiké gyorsul:

\begin{matrix} ω_{1 c} r = v_{0} - \frac{μ_{1} g}{Φ} \cdot t, ω_{2 c} r = \frac{μ_{2} g}{Φ} \cdot t . \end{matrix}

Mindez addig tart, amíg a 2. golyó kerületi sebessége el nem éri a középpontok közös sebességét

(d)

állapot. Az az időpont:

\begin{matrix} t_{bd} = \frac{v_{0}}{g} \cdot \frac{Φ m_{1}}{Φ (μ_{2} m_{2} - μ_{1} m_{1}) + μ_{2} (m_{1} + m_{2})} . \end{matrix}

Ekkor:

\begin{matrix} v_{1 d} = v_{2 d} = ω_{2 d} r = v_{0} \cdot \frac{μ_{2} m_{1}}{Φ (μ_{2} m_{2} - μ_{1} m_{1}) + μ_{2} (m_{1} + m_{2})}, \end{matrix}

az első golyó még mindig köszörül, kerületi sebessége ekkor

\begin{matrix} ω_{1 d} r = v_{0} - v_{0} \cdot \frac{μ_{1} m_{1}}{Φ (μ_{2} m_{2} - μ_{1} m_{1}) + μ_{2} (m_{1} + m_{2})} . \end{matrix}

Az ezután következő szakaszban

(e)

a hátsó golyó még mindig köszörül, lenn

μ_{1} m_{1} g

súrlódási erő működik. Ezzel mindkét golyó középpontját gyorsítja és az elöl levő (2) golyót felpörgeti úgy, hogy a golyók továbbra is együtt maradnak és a 2. golyó simán gurul. Most a 2. golyó alsó érintkezési pontján

X

súrlódási erő lép működésbe.

X

kiszámítására egyenlővé tesszük a középpontok gyorsulását a 2. golyó kerületi gyorsulásával:

\begin{matrix} \frac{μ_{1} m_{1} g - X}{m_{1} + m_{2}} = \frac{X}{Φ m_{2}} . \end{matrix}

Innen

\begin{matrix} X = \frac{Φ μ_{1} m_{1} m_{2} g}{m_{1} + m_{2} + Φ m_{2}} . \end{matrix}

Bizonyítható, hogy

X < μ_{2} m_{2} g

, tehát keletkezhet ekkora súrlódási erő.
Ebben a szakaszban:

\begin{matrix} v_{1 e} = v_{2 e} = ω_{2 e} r = v_{0} \frac{μ_{2} m_{1}}{Φ (μ_{2} m_{2} - μ_{1} m_{1}) + μ_{2} (m_{1} + m_{2}} + \frac{μ_{1} m_{1}}{m_{1} + m_{2} + Φ m_{2}} g t . \end{matrix}

t

időt most

d

-állapottól számítjuk.

ω_{1} r

az eddigi ütemben csökken.
A végső

(f)

állapot akkor következik be, amikor az 1. golyónál is beáll a sima gördülés. Ennek időtartama a

d

-állapottól számítva:

\begin{matrix} t_{df} = \frac{v_{0}}{μ_{1} g} \cdot \frac{m_{1} + m_{2} + Φ m_{2}}{m_{1} + m_{2}} \cdot \frac{Φ (μ_{2} m_{2} - μ_{1} m_{1})}{Φ (μ_{2} m_{2} - μ_{1} m_{1}) + μ_{2} (m_{1} + m_{2})} . \end{matrix}

Ekkor mindkét golyóra nézve létrejön a sima gördülés a közönséges rugalmatlan ütközés (már

b

-ben meglevő) sebességével:

\begin{matrix} v_{1 f} = v_{2 f} = ω_{1 f} r = ω_{2 f} r = k v_{0} . \end{matrix}

A folyamat teljes ideje:

\begin{matrix} t_{bf} = t_{q} t e x t b d + t_{df} = \frac{v_{0} Φ m_{2}}{μ_{1} g (m_{1} + m_{2})}, \end{matrix}

függetlenül

μ_{2}

-től.
Ha

μ_{1} m_{1} > μ_{2} m_{2}

, akkor a középpontok sebessége először felgyorsul és először az 1. golyó éri el a sima gördülést, majd a középpontok sebessége újra lassul és a végállapotban valamennyi sebesség újra

k v_{0}

. Az erre az esetre vonatkozó képletek hasonló módon vezethetők le. A sebességek ismeretében mindkét esetben könnyen számítható a mozgási energiák változása. Ha

ω_{1} m_{1} = μ_{2} m_{2}

, akkor a versenyfeladatban szereplő egyszerű eset áll fenn.
Numerikus adatok néhány esetben.

\begin{matrix} m_{1} & 100 & 100 & 100 & 300 & 300 \\ m_{2} & 100 & 300 & 100 & 100 & 100 \\ μ_{1} & 0, 02 & 0, 02 & 0, 04 & 0, 02 & 0, 02 \\ μ_{2} & 0, 04 & 0, 02 & 0, 02 & 0, 02 & 0, 04 \\ k v_{0} & 0, 5 v_{0} & 0, 25 v_{0} & 0, 5 v_{0} & 0, 75 v_{0} & 0, 75 v_{0} \\ t_{bd} v_{0} / g-ben & 50 / 11 & 35 / 6 & 50 / 11 & 25 / 6 & 50 / 11 \\ t_{bf} v_{0} / g-ben & 10 & 15 & 10 & 15 & 7, 5 \\ v_{1 d} = v_{2 d} v_{0}-ban & 5 / 11 & 5 / 24 & 6 / 11 & 19 / 24 & 17 / 22 \end{matrix}