Kezdőlap


Feladat:	642. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ferencz László , Maróti Péter
Füzet:	1967/május, 233 - 234. oldal		PDF \| MathML
Témakör(ök):	Összetartó erők eredője, Feladat
Hivatkozás(ok):	Feladatok: 1966/december: 642. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A rendszer ott van nyugalomban, ahol a kötelekre ható erők eredője nulla. Az 500 p-os erőt az $a$ és $b$ szárakban fellépő 300 p és 400 p nagyságú erők tartják egyensúlyban. Minthogy ezeknek az erőknek aránya $3 : 4 : 5$ , Pythagoras tétele alapján következik, hogy az ezekből képzett vektorháromszög derékszögű. Így a kötelek metszéspontja az $A B = 80$ cm hosszú szakasz Thales‐körén helyezkedik el (1. ábra).

1. ábra

A vektorháromszög és az

A B X

háromszög hasonlóságából következik, hogy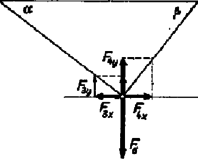

\begin{matrix} 3 : 4 : 5 = b : a : 80, amiből \\ a = 64 cm és b = 48 cm . \end{matrix}

Továbbá a

\begin{matrix} 3 : 4 : 5 = x : m : 48 arányosságból \\ x = 28, 8 cm, m = 38, 4 cm . \end{matrix}

Ferencz László (Bp., Fazekas M. g. II. o. t.)

Megjegyzés. A feladat szövegében az ábrával ellentétben 500 p helyett 50 p szerepelt. Nyilvánvalóan az ábra adata volt jó, mert 50 p esetén nincs is egyensúlyi helyzet.

2. ábra

II. megoldás. Az egyensúly feltétele (2. ábra)

\begin{matrix} F_{3 y} + F_{4 y} - F_{5} = 0, - F_{3 x} + F_{4 x} = 0. \end{matrix}

A szögösszefüggéseket beírva

\begin{matrix} F_{3} \cdot sin α + F_{4} \cdot sin β = F_{5}, F_{4} \cdot cos β = F_{3 x} cos α . \end{matrix}

Az első egyenlet második tagját a jobb oldalra visszük és mindkét egyenletet négyzetre emelve kapjuk

\begin{matrix} F_{3}^{2} sin^{2} α = F_{5}^{2} - 2 F_{4} F_{5} \cdot sin β + F_{4}^{2} \cdot sin^{2} β, \\ F_{3}^{2} \cdot cos^{2} α = F_{4}^{2} cos^{2} β . \end{matrix}

A két egyenletet összeadva, figyelembe véve, hogy

sin^{2} α + cos^{2} α = 1

, és

sin β

-t kifejezve kapjuk

\begin{matrix} sin β = \frac{1}{2 \cdot F_{4} \cdot F_{5}} (F_{5}^{2} + F_{4}^{2} - F_{4}^{2}) Így \\ sin β = 0, 8, β = 53, 13^{\circ} . \end{matrix}

Az egyenletek szimmetriája miatt

α

értékét megkapjuk, ha a végösszefüggésben 4 és 3 indexeket felcseréljük. Így

\begin{matrix} sin α = 0, 6, α = 36, 87^{\circ} . \end{matrix}

α

és

β

szögek ismeretében a többi adat kiszámítható.

Maróti Péter (Szeged, Ságvári E. g. II. o. t.)

Megjegyzés. Figyeljük meg, hogy ez a megoldás nem használja fel a Pythagoras tételt, így általános esetben is használható.