Kezdőlap


Feladat:	637. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kele András , Molnár Gyula
Füzet:	1967/április, 188 - 189. oldal		PDF \| MathML
Témakör(ök):	Izotermikus állapotváltozás (Boyle--Mariotte-törvény), Gázok egyéb állapotváltozása, Feladat
Hivatkozás(ok):	Feladatok: 1966/november: 637. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. A dugattyú akkor van nyugalomban, ha a két hengerben a nyomás egyenlő. Jelöljük az elmozdulást $x$ -szel. Az ábra jelölései a kiinduló értékeket jelzik. A melegített tartályban a nyomás $p_{0}$ -ról $p_{1}$ -re, a hőmérséklet $T_{0}$ -ról $T_{1}$ -re, a térfogat $V_{0} = F \cdot h$ -ról $V_{1} = F \cdot (h + x)$ -re változik. Az általános gáztörvény szerint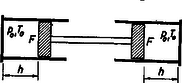

\begin{matrix} \frac{F \cdot h \cdot p_{0}}{T_{0}} = \frac{F \cdot (h + x) \cdot p_{1}}{T_{1}} . \end{matrix}

A másik hengerben a hőmérséklet nem változik, ezért a Boyle‐Mariotte-törvény alapján

\begin{matrix} F \cdot h \cdot p_{0} = F \cdot (h - x) \cdot p_{1} . \end{matrix}

A két egyenletből

\begin{matrix} x = \frac{h \cdot (T_{1} - T_{0})}{T_{1} + T_{0}} = \frac{25 cm \cdot 150^{\circ} K}{696^{\circ} K.} = 5, 39 cm, \end{matrix}

és a nyomás a hengerekben

\begin{matrix} p_{1} = P_{0} \cdot \frac{T_{1} + T_{0}}{2 \cdot T_{0}} = 1 at \frac{696^{\circ} K}{546^{\circ} K} = 1, 275 at . \end{matrix}

(Eltekintünk a fizikai és légköri atmoszféra különbségétől.)

2. Az előbbiekben felmelegített hengert most állandó térfogaton az eredeti hőmérsékletre hűtjük. A nyomás

p_{1}

-ről

p_{2}

-re csökken. Gay-Lussac törvénye értelmében

\begin{matrix} p_{2} = \frac{p_{1} \cdot T_{0}}{T_{1}} = \frac{1, 275 at \cdot 273^{\circ} K}{423^{\circ} K} = 0, 823 at . \end{matrix}

A másik hengerben a nyomás

1, 275 at

maradt, ezért a nyomóerő, amit ki kell egyenlíteni:

\begin{matrix} P = F \cdot (p_{1} - p_{2}) = 300 {cm}^{2} \cdot 0, 452 at = 135, 6 kp . \end{matrix}

Ha a légköri nyomás pontosabb értékét figyelembe vesszük,

P = 140, 1 kp

.
A fenti kifejezésben

p_{1}

és

p_{2}

értékét beírva megkaphatjuk a nyomóerő általános kifejezését is:

\begin{matrix} P = \frac{F \cdot p_{0} \cdot (T_{1}^{2} - T_{0}^{2})}{2 \cdot T_{1} \cdot T_{0}} . \end{matrix}

3. Ha a melegített hengert állandó térfogaton tartjuk, akkor a nyomás

p_{0}

-ról

p

-re növekszik:

\begin{matrix} p = \frac{p_{0} \cdot T_{1}}{T_{0}} = \frac{1 at \cdot 423^{\circ} K}{273^{\circ} K} = 1, 55 at . \end{matrix}

A másik oldalon is ekkora nyomást kell elérni. Azonos térfogat mellett és azonos hőmérsékleten a nyomás és a gáz tömege egyenesen arányos.
A szükséges térfogatnövekedés normálállapotú levegőre vonatkoztatva

\begin{matrix} V = V_{0} \cdot \frac{p - p_{0}}{p_{0}} = \frac{T_{1} - T_{0}}{T_{0}} \cdot V_{0} = 0, 55 \cdot 7500 {cm}^{3} = 4125 {cm}^{3}, \end{matrix}

aminek tömege

m = 5, 32 g

Molnár Gyula (Hajdúszoboszló, Hőgyes E. g. III. o. t.)
Kele András (Nagykanizsa, Landler J. g. III. o. t.)