Kezdőlap


Feladat:	634. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bálványos Zoltán , Faragó László , Farkas János , Gilyén Péter , Herendi Ágnes , Marossy László , Maróti Péter , Mihályfi László , Nádai László , Sághy András , Stefanovicz Károly , Trencséni Sándor , Vad Kálmán
Füzet:	1967/április, 184 - 186. oldal		PDF \| MathML
Témakör(ök):	Egyéb kényszermozgás, Nyomóerő, kötélerő, Összetartó erők eredője, Feladat
Hivatkozás(ok):	Feladatok: 1966/november: 634. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A pontszerű testre három erő hat: az $F_{A}$ és $F_{B}$ húzóerők és a körpálya $K$ kényszer- (ellen-)ereje, amely a körpályán tartja a testet (1. ábra). Mivel az $F_{A}$ és $F_{B}$ erők arányosak a $P A$ és $P B$ távolságokkal, az ábra léptékét úgy választhatjuk meg, hogy az $F_{A}$ és $F_{B}$ erőket éppen $P A$ és $P B$ hosszúságú szakaszokkal ábrázoljuk.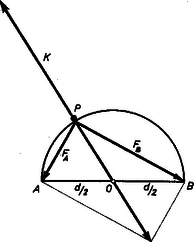

1. ábra

Thales tétele szerint

F_{A}

és

F_{B}

eredője éppen átmegy a kör középpontján. Mivel a test nem hagyhatja el a körpályát (a testnek nem lehet sugárirányú gyorsuláskomponense), a

K

kényszererőnek olyan nagynak kell lennie, mint az

F_{A}

és

F_{B}

eredője. A testre ható erők eredője éppen nulla a körpálya minden pontjában, tehát a nyugalomban levő pontszerű test továbbra is nyugalomba marad. (Egyensúlyi helyzete közömbös.) A gondolatmenet az

A

és

B

pontokban is érvényes.

Sághy András (Bp., Apáczai Csere J. gyak. g. II. o. t.)
dolgozata alapján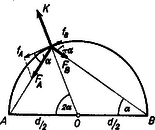

2. ábra

II. megoldás. A feladatot számítással is megoldhatjuk (2. ábra). Számítsuk ki a testre ható erők eredőjének érintő irányú komponensét. (A sugárirányú komponens nyilván nulla.) A két arányossági tényező legyen

k_{A}

és

k_{B}

. Ekkor:

\begin{matrix} P A = d \cdot sin α; P B = d \cdot cos α; \end{matrix}

\begin{matrix} F_{A} = k_{A} \cdot P A = k_{A} \cdot d \cdot sin α; \end{matrix}

\begin{matrix} F_{B} = k_{B} \cdot P B = k_{B} \cdot d \cdot cos α . \end{matrix}

Az érintő irányú komponensek:

\begin{matrix} f_{A} = F_{A} \cdot cos α = k_{A} \cdot d \cdot sin α \cdot cos α = 1 / 2 k_{A} \cdot d \cdot sin 2 α, \\ f_{B} = F_{B} \cdot sin α = k_{B} \cdot d \cdot cos α \cdot sin α = 1 / 2 k_{B} \cdot d \cdot sin 2 α . \end{matrix}

(A kényszererőnek nincs érintő irányú komponense.)

Így a nyugalomban levő pontra ható eredő erő:

\begin{matrix} f = f_{A} - f_{B} = 1 / 2 (k_{A} - k_{B}) d sin 2 α . \end{matrix}

k_{A} = k_{B}

(mint azt az I. megoldásban feltételeztük):

f = 0

, vagyis

α

-tól függetlenül (a körpálya minden pontjában) a test nyugalomban marad. Ha például

k_{A} > k_{B}

(az

A

pontból ható erő arányossági tényezője nagyobb, vagyis az

A

,,rugó'' erősebb),

f

A

pont felé gyorsítja a testet. Tehát ekkor csak az

A

és a

B

pontokban

(sin 2 α = 0)

marad nyugalomban a test, a többi helyen gyorsuló mozgást végez. A gyorsulás maximális akkor, ha

sin 2 α

maximális, vagyis ha

2 α = 90^{\circ}

Stefanovicz Károly (Bp., Veres Pálné g. II. o. t.) és
Vad Kálmán (Jászberény, Lehel vezér g. II. o. t.)
dolgozata alapján

Megjegyzések. 1. Mivel a gömb egy átmérőjének két végpontja és a gömb felületének egy pontja által meghatározott sík egy körben metszi a gömböt, a feladat gömb esetére is általánosítható.

Nádai László (Bp., Fazekas M. gyak. g. II. o. t.)

2. Ha tudjuk, hogy a rugó potenciális energiája

1 / 2 k x^{2}

, ahol

x

a megnyúlás és

k

a rugóállandó (egységnyi kitérést létrehozó erő), akkor a megoldás így is nyerhető.
Az összes potenciális energia:

E_{p} = 1 / 2 P A^{2} + 1 / 2 k P B^{2} = 1 / 2 k (P A^{2} + {P B}^{2}) = 1 / 2 k d^{2}

‐ állandó. Mivel a rendszer mindig úgy akar mozogni, hogy a potenciális energiája csökkenjen, ebben az esetben nem indul el a test. Látható, hogy ha pl.

k_{A} > k_{B}

, a potenciális energia akkor minimális, ha a test az

A

pontban van, vagyis a test csak itt van nyugalomban.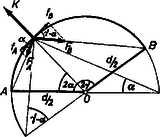

3. ábra

3. Ha az

A

és a

B

pont nem a kör egyik átmérőjének két végpontja, hanem az

A O B

szög

2 γ \neq 180^{\circ}

nagyságú, a feladatot a II. megoldáshoz hasonlóan megoldhatjuk (3. ábra):

\begin{matrix} P A = d \cdot sin α; P B = d \cdot cos (γ - α); \\ F_{A} = k_{A} P A = k_{A} \cdot d \cdot sin α; \\ F_{B} = k_{B} P B = k_{B} \cdot d \cdot cos (γ - α) . \end{matrix}

Az érintő irányú komponensek:

\begin{matrix} f_{A} = F_{A} cos α = 1 / 2 k_{A} \cdot d \cdot sin 2 α; \\ f_{B} = F_{B} sin (γ - α) = 1 / 2 k_{B} \cdot d \cdot sin 2 (γ - α) . \end{matrix}

Az eredő erő:

\begin{matrix} f = f_{A} - f_{B} = \frac{d}{2} [k_{A} sin 2 α - k_{B} sin 2 (γ - α)] . \end{matrix}

k_{A} = k_{B} = K

, akkor

\begin{matrix} f = \frac{k d}{2} [sin 2 α - sin 2 (γ - α)] = k d cos γ sin (2 α - γ) \end{matrix}

(sin x - sin y)

-ra vonatkozó összefüggés segítségével

].
A test csak az

f = 0

esetben marad nyugalomban, vagyis ha

2 α = γ

. Tehát a test csak az

A B

ív felezőpontjában marad nyugalomban, különben pedig a felezőpont felé gyorsul a körív mentén. Ezek csak akkor igazak, ha

cos γ \neq 0 (2 γ \neq 180^{\circ})

, mivel ha

2 γ = 180^{\circ}

f

és a gyorsulás is

α

-tól függetlenül nulla.
A

k A \neq k B

esetben a megoldás teljesen hasonló lesz, csak az egyensúlyi helyzet nem a körív felezőpontja:

\begin{matrix} k_{A} sin 2 α - k_{B} sin 2 (γ - α) = 0, \end{matrix}

innen

\begin{matrix} tg 2 α = \frac{k_{B} sin 2 γ}{k_{A} + k_{B} cos 2 γ} \end{matrix}

az egyensúlyi helyzetben.

Faragó László (Bp., Fazekas M. g. II. o. t.)

4. A legtöbb megoldásban nem szerepel a kényszererő, hanem azt ,,a test nyugalomban van akkor, ha a rá ható összes erők eredője sugárirányú'' kijelentéssel helyettesítették. Ilyen szempontból a feladat szövege sem helyes (,,más erő nem hat rájuk'').