Kezdőlap


Feladat:	610. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Herendi Ágnes
Füzet:	1966/december, 239. oldal		PDF \| MathML
Témakör(ök):	Tömegpont egyensúlya, Nyomóerő, kötélerő, Feladat
Hivatkozás(ok):	Feladatok: 1966/május: 610. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Foglalkozzunk általánosabban a problémával. Legyen a fonál hossza $L = n R$ . Ekkor a tömegekhez vezető rádiuszok által bezárt $φ$ szög (lásd az ábrát) szintén ismeretes: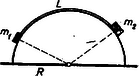

\begin{matrix} φ_{fok} = \frac{180}{π} \cdot \frac{L}{R} = \frac{180}{π} \cdot n, φ_{rad} = \frac{L}{R} = n . \end{matrix}

φ

-t ezentúl mint ismert adatot kezeljük.

A szerkezet helyzetét az

m_{1}

tömeghez vezető rádiusz

α

szögével határozzuk meg.

m_{1}

tömeg

(90^{\circ} - α)

hajlásszögű lejtőn van, tehát az érintő mentén kifejt

m_{1} g sin (90^{\circ} - α) = m_{1} g cos α

húzóerőt.

m_{2}

tömeg

(α + φ - 90^{\circ})

-os hajlás szögű lejtőn van, tehát az érintő mentén kifejt

m_{2} g s i n (α + φ 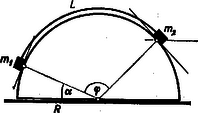- 90^{\circ}) = - m_{2} g cos (α + φ)

húzóerőt.

Az egyensúlyt a húzóerők egyenlősége jelenti:

\begin{matrix} m_{1} g cos α = - m_{2} g cos (α + φ), \end{matrix}

kifejtve:

\begin{matrix} - m_{2} (cos α cos φ - sin α sin φ) = m_{1} cos α . \end{matrix}

Osztva

cos α

-val (mely nem lehet 0):

\begin{matrix} m_{2} sin φ tg α = m_{1} + m_{2} cos φ . \end{matrix}

Ennek

α

-ra történő megoldása határozza meg az egyensúlyi helyzetet:

\begin{matrix} tg α = \frac{\frac{m_{1}}{m_{2}} + cos φ}{sin φ} . \end{matrix}

A fonálerő:

\begin{matrix} P = m_{1} g cos α = \frac{m_{1} g sin φ}{\sqrt[]{1 + 2 \cdot \frac{m_{1}}{m_{2}} \cdot cos φ + {(\frac{m_{1}}{m_{2}})}^{2}}}, \end{matrix}

ugyanis

cos α = 1 / \sqrt[]{1 + tg^{2}α}

.
Az egyensúlyi helyzet labilis, mert például

α

csökkenésekor

m_{1}

húzó összetevője nagyobb,

m_{2}

húzó összetevője kisebb lesz, és az egész szerkezet még inkább balra csúszik.
A mi számadatainkkal

n = 2, φ = 114, 6^{\circ}, tgα=0,0921

és

α = 5, 26^{\circ}

; a fonálerő

P = 9, 955 kp

.
Megoldható a feladat

m_{1}

és

m_{2}

közös súlypontjával, amely egy köríven mozog. Az jelenti a labilis egyensúlyi helyzetet, ha ez a súlypont félkörös pályájának a tetőpontján van.

Herendi Ágnes (Bp., Toldy F. g. I. o. t.)